We use algebra constantly in our daily lives, yet most of us don’t know its roots. It originated in ancient Babylon because they found a way to solve linear and quadratic equations without the use of geometric solutions which were the norm of the time. At the close of the 16th century, François Viète, a French mathematician, furthered algebra by including variables and letters as parameters. Since then, algebra has been divided into subgroups such as Abstract Algebra, Linear Algebra, Boolean Algebra, and Algebraic geometry. These subgroups all circulate the manipulation of symbols in their respective fields. Universal Algebra in particular is unlike other studies of algebra that study models of different algebraic structures, but it studies the broader applications of algebraic structures.

How ancient Babylonians used Algebra to calculate side lengths. | Source: JSTOR
History of Universal Algebra
In 1898, English mathematician and philosopher Alfred North Whitehead published A Treatise of Universal Algebra which gave a formal definition that is still used now for universal algebra. Because of the development of new algebraic structures, they required expansion beyond communicative classes.
In a review, Alexander Macfarlane wrote that “The main idea of the work is not unification of the several methods, nor generalization of ordinary algebra so as to include them, but rather the comparative study of their several structures.” In the early-mid 1900s, Garrett Birkhoff developed theories on lattice theory and universal algebra, explaining its components. Birkhoff pioneered a new understanding of free algebra and his work has continued to evolve with category theory.
Conceptual Understanding
Algebra taught in schools uses numbers and their basic arithmetic operators (+, −, ×, ÷) along with symbols that hold the value of a number and variables. Expanding on the topics learned in elementary algebra, algebra’s essence lies in using predefined finitary operations on a non-empty set. An algebraic structure is a pair, A = (A, F), where A is a non-empty set called the universe.
In its essence, universal algebra analyzes the workings of all algebraic structures including, rings, lattices, fields, etc. The rules in universal algebra are better visualized when applied to a set A and the operations that manipulate it. The operations, which are denoted by n-ary operation, n being a number, are functions that take an element from A and return a single output. If n is 0, it is called a 0-ary operation (null operation) and returns a constant. If it is 1-ary operations (unary operation), its operations are negations. This is denoted by placing a symbol in front of the argument: ~x. Also, 2-ary operations (binary operations) include addition, subtraction, exponentiation, multiplication, division, and trigonometric functions. For higher n-ary operations, the arguments are placed in the roster method of the function, f(x,y,z). After the operations are defined, the axioms set the algebraic laws and limitations of set A.
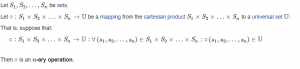
A formal definition of n-ary operations. | Source: Wikipedia
Structural Understanding
Stanley Burris’ A Course in Universal Algebra defines a variety as, “A collection of algebraic structures defined by identities is called a variety or, equational class.” This creates restrictions on the identities used in universal algebra, letting its applicability to algebraic structures have a wider scope.
Universal algebra is characterized by category theory. Instead of listing out the operations assigned to the different sets, it uses algebraic theories. Algebraic theories use what is known as “free variables” which are a kind of placeholder and create equations to define the axioms of the set. Recently, it has been characterized through operad theory. Operad uses a set of operations (addition, subtraction, multiplication, etc.) similar to universal algebra, but there are limits on communicative properties that are not the same.
Why?
Universal algebra to the untrained eye is another extraneous field of algebra that is unimportant if learning specific fields of algebra. Which may lead you to question “Why should I have to learn about the broad structure for the specific structures I want to learn about?” Its significance lies in extracting common elements of seemingly different algebras and giving important theorems that prove things in all fields of algebra. For example, the isomorphism theorems had four crucial theorems that explain congruency among different subsets, which could then be applied to all of the other algebraic structures. This creates a framework that is universal (pun intended!) when dealing with different algebraic structures and greatly helps when conceptualizing them.





Be the first to comment on "An Introduction to Algebra’s Universe"