Reaffirming an Anomaly: Baksan Experiment on Sterile Transitions

Experimental data from the Baksan Experiment on Sterile Transitions (BEST) confirms a deficit of electron neutrinos (\(\nu_e\)) observed in previous radiochemical measurement at the SAGE (1990–2007) and GALLEX (1998–2003) experiments. BEST, like the two prior experiments, used the scattering interaction between electron neutrinos and gallium (\(\text{Ga}\)) targets to induce the production of germanium (\(\text{Ge}\)). The discrepancy between the theoretical and experimental predictions for \(\text{Ge}\) is dubbed the gallium anomaly. The BEST results for the measured rate of \(\text{Ge}\) production suggests a lower than expected presence of electron neutrinos, with production ratios (\(R =\) measured\(/\)expected) of \(R_{\text{in}} = 0.79 \pm 0.05\),  \(R_{\text{out}} = 0.77 \pm 0.05 \).

Theoretical Motivation

Initial theoretical predictions suggested all three flavors of neutrinos were massless. However, evidence of neutrino oscillations between its flavors at the Liquid Scintillator Neutrino Detector at Los Alamos (LSND) suggested that at least two out of the three flavors must be massive and exclusively different.

The non-zero mass prediction arises from the mathematical description of the neutrino’s defining characteristics. As with all other Standard Model (SM) elementary particles, the quantum mechanical eigenstates that form the basis of neutrino properties at observation rely on a wave function (and thus are in superposition until measurement). The flavor-determining eigenstates of the neutrino are superpositions of mass eigenstates, with the latter having individually different time evolutions.

These mass eigenstates must be intrinsically unique to allow for oscillation, otherwise violating Pauli’s exclusion principle (as neutrinos are spin-\(1/2\) particles), suggesting at least two have non-zero mass. It is commonly assumed that all three are non-zero and different. Although the number of mass eigenstates (which corresponds to the number of neutrino flavors) must be at least three by the SM, a definitive number remains unknown and subject to experimental observation and theoretical description.

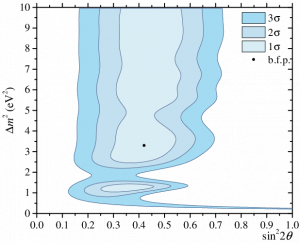
The results of BEST experimental exclusion with deviation for a large mass difference (\(\Delta m^2\)) between the Standard Model electron neutrino (\(\nu_e\)) and a theoretical sterile neutrino (\(\nu_s\)), along with a large mixing angle (\(\sin^22\theta\)) for the transition | Source: CERN

The behavior of neutrino oscillations between its three current SM flavors (electron, muon, and tau neutrino) is yet to have a satisfactory definition, largely due to the propositions resulting from conflicting experimental results at LSND, MiniBooNE, SAGE, and GALLEX.

The gallium anomaly—and more specifically the deficit of electron neutrinos—could suggest a fourth neutrino mass eigenstate (and thus flavor), frequently called the sterile neutrino. However, other experiments such as MicroBooNE, IceCube, and MINOS+ did not find any anomalous oscillation to provide evidence for transitions to a fourth sterile flavor. The plethora of conflicting experimental data, though with varying levels of statistical significance, and incomplete theoretical framework necessitate further experimentation.

Experiment Methodology

In order to better understand the anomalous oscillation observed in gallium-based experiments, physicists from Los Alamos National Laboratory (LANL) and the Institute for Nuclear Research of the Russian Academy of Sciences (INR RAS) collaborated on BEST. The experiment is located more than a mile underground within the Baksan Neutrino Observatory in the Caucasus Mountains (RUS).

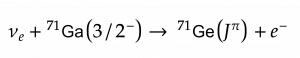
Detection of the electron neutrinos for transition evidence is achieved using charged-current neutrino nucleus scattering dictated by the chemical transformation of Ga to Ge. The scattering cross section for ground state (\(175\) \(\text{keV}\)) and excited state (\(500 \text{ keV}\)) in Ge are higher in microscopic nuclear model, than during observations in BEST | Typesetting: Dheeran Wiggins | Source: The gallium anomaly revisited (Kostensalo et. al.)

BEST takes advantage of a scattering-based chemical reaction that occurs when exposing \(\text{Ga}\) to a source of electron neutrinos, resulting in \(\text{Ge}\) and electrons. The preceding experiments SAGE and GALLEX first used a solar \(pp\) chain neutrino source to initiate the reaction, and later confirmed the sensitivity of the study using strong radiative electron-capture sources \((^{51}\text{Cr}\) and \( ^{37} \text{Ar})\) placed at the center of the \(\text{Ga}\) targets.

Additionally, because SAGE and GALLEX used a single \(\text{Ga}\) target each, the measured \(\text{Ge}\) production rates were compared only to theoretical expectation values. On the other hand, BEST uses a two-target system placed in a concentric fashion, with a spherical interior and cylindrical exterior. The source of electron neutrinos \((^{51}\text{Cr})\) was placed within the interior of the spherical target, removing the use of a solar \(pp\) chain neutrino source. Thus, the \(\text{Ge}\) production could be measured at two distances from the internally placed, irradiating \(^{51}\text{Cr}\).

A ratio of each measured value against the theoretical prediction \((R)\) was calculated yielding \( R_{\text{in}} = 0.79 \pm 0.05 \), \(R_{\text{out}} = 0.77 \pm 0.05\)). The ratio of the production values at each distance \((R_{\text{in}}/R_{\text{out}})\) resulted in an accuracy measure of \(0.97 \pm 0.07\) (where values approaching \(1.00 \pm 0.00\) suggest higher accuracy). The rates were similar and fit comparative predictions in relation to one another. As with SAGE and GALLEX, the rates themselves were lower \((20–24\%)\) than the theoretical predictions suggested, reaffirming the presence of an anomalous behavior. This implies the possibility of the lower count of electron neutrinos being a result of some transitioning to a fourth sterile flavor.

The results of the experiment were then applied to theoretical models of electron neutrino to sterile neutrino oscillations (\(\nu_e \to \nu_s\)) using a mass square difference of \(\Delta m^2 > 0.5 \text{eV}^2\) and a mixing of \(\sin^22\theta \approx 0.4\).

A Brief Aside: Experimental Values in Neutrino Physics

The mass difference between two flavors in a neutrino transition (\(\nu_e \to \nu_s\)), assuming oscillation in a vacuum, can be represented as \(\Delta m^2_{e,s} = m_e^2 – m^2_s\). Experiments seek to narrow down the masses of the flavors with newer high-energy runs at major accelerators (or more low-energy experiments like BEST), along with improved statistical analyses. Thus, the masses of the flavors remains a question of upper and lower limits, meaning \(\Delta m^2\) is usually depicted in papers using an inequality. The mixing angle is an angle between the orthogonal QM basis vectors of the involved eigenstates. The basis states for the mass eigenstates of the Hamiltonian (\(\nu_1, \nu_2\), and \(\nu_3\)) and the states for the weak eigenstates of the Hamiltonian (\(\nu_e, \nu_\mu\), and \(\nu_\tau\)) are rotationally related because they are orthonormal, despite generally being not orthogonal to the interacting states. The three-dimensional rotations in this system are known as the mixing angles \(\theta_{12}, \theta_{23}\), and \(\theta_{13}\), which are described using the Pontecorvo-Maki-Nakagawa-Sakata (PMNS) matrix.

When the state shifts after time evolution and is decomposed at \(t=T\) (using respective phase factors from Schrödinger’s equation), the observable effect is neutrino oscillation. Thus, the majority of experiments regarding neutrino oscillation or sterile transitions include inequality limits for mass difference and approximate values for a mixing angle that would facilitate the potential transition. The values can then be used by theoretical physicists to reformulate the SM symmetries and Lagrangians to account for the anomalous behavior.

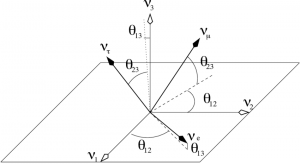
Assuming no violation of charge-parity (CP), the mixing angles for neutrinos can be represented as Euler angles in a three-dimensional space, relating the two sets of interacting basis states. CP violation results in an oscillation phase change which must be accounted for when investigating mixing angles in sterile transitions | Source: Neutrino Mass and Mixing in the Seesaw Playground* (King)

Future Prospects

Results from BEST and MiniBooNE, alongside future results from experiments such as the Deep Underground Neutrino Experiment (DUNE) at LBNF (Fermilab), will be used to further investigate the anomalous neutrino behavior. Many theoretical interpretations of the data suggest a fourth sterile transition, proposing a potential candidate for dark matter. Alternative explanations—such as extensive reformulations of the current SM three-neutrino model—attempt to find a missing piece (whether within the mathematics, or within other experimentally observed phenomena) to satisfy the anomaly. As experimental evidence for anomalous neutrino oscillation behavior accumulates, magnifying a flaw in the contemporary theory, the prospects for new physics increase expansively.