By: Andrew D. Katson

Definition

Category theory, as invented in 1945, is a field of mathematics that works with objects and their relationships. A category is a set made up of multiple elements, called “objects”, and their “mappings” (5, 11). In figure 1, we see that X, Y, and Z are elements, and f, g, and their composition, g(f), are mappings. There are properties that every category must exhibit. These include (5, 11):

• An identity mapping, e, which maps an element to itself, see Fig. 2
• Mappings must exhibit the associative property, namely, a(bc)=(ab)c

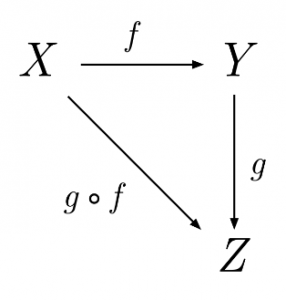
Fig. 1: A basic category diagram (Source: Wikipedia Commons.)

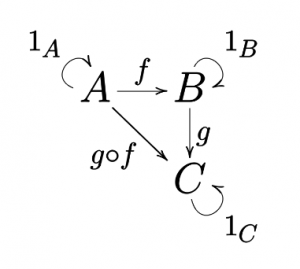
Fig. 2: A basic category diagram with identity mappings 1a, 1b, and 1c labeled (Source: Wikipedia Commons.)

Category theory further defines other abstract ideas with more specific characteristics, such as “abstract” categories and “concrete” categories, but all in all: they are just sets with specific characteristics.

N-dimensional Categories

We may define a category of n dimension by considering the conceptual ideas of a standard category. In a normal category, we have objects, the rules they obey, and the relationships they exhibit. If we say a set contains all the real multiples of 2, then that may be our relationship. Hence, we define these terms (6): 0-Cells, the objects of the category, 1-Cells, the relationship between the objects, 2-Cells, the relationship between the relationships of the objects, 3-Cells, the relationship between relationships between relationships of the objects, and rules, which the objects must obey. But of course, rules too may be subject to rules. In a given system, we may say “the rules bounding the objects must all be of this form”, thus providing restrictions for the rules. Hence, a similar concept must apply to the rules. Furthermore, the amount of rules needed for rules depends on how “strict” the rules are (6). And all this from the simple realization of how sets work. 

Examples of categories

We have now defined a category, but we still don’t know why this abstraction is useful. It may help us to see what sets may be defined as categories. It may be proved that all of the following are categories (5, 11):

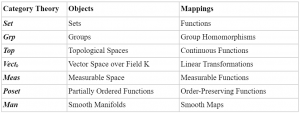
Fig. 3: Examples of Categories, along with their objects and mappings.

And many, many more! The reader need not know what each of these examples are, just that they are all categories: they all have objects with mappings that move between these objects. However, the examples above do demonstrate that most mathematical ideas may be expressed as some form of a category. It is here that the true elegance of the category is found: the ability to express mathematical fields as their own separate structure, and then combine them via an overarching idea. For example, in Fig 3, we link linear algebra (Vectₖ), abstract algebra (Grp), topology (Top),  and foundational mathematics (Set) under one unifying property– they’re all categories. 

Applications

The applications of category theory are growing constantly. As of now, category theory has found applications in data modeling (4), machine learning (7), linguistics, computer science, physics (2, 3), biology (9, 10), mathematics, economics (8), and even in defining the scientific method itself (1). Understanding “the math of mathematics” helps us develop any science that may include the presence of mathematics. Category theory also uses simplistic diagrams to express complex ideas. These diagrams happen to look very similar to that of other sciences. For example, in data modeling, we may use a diagram such as in Fig. 4. In category theory, we define a “directed multigraph” to help us transform something like Fig. 5, into a mathematical object because many types of graphs happen to be categories (4). 

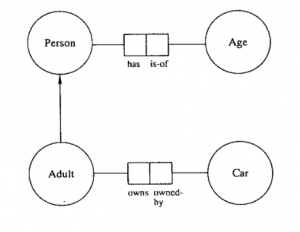
Fig. 4: An example of a basic Data Modeling diagram. (4)

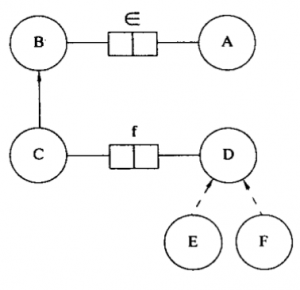
Fig 5: A possible directed multigraph, which is a category, for data modeling. (4)

Because of the similarity between these diagrams, one may rapidly construct a category and hence apply category theory to determine the significance of their diagram. Since categories can take many, many forms, we can explore many fields of science and mathematics, link them together, and push the boundaries of our understanding. 

Summary

Today, category theory is a promising field of mathematics, with modern applications to just about any field of science. Its abstractive properties allow for the joining of vastly distinct mathematics. And despite these achievements, its definitions remain clear, elegant, and straightforward: a category is nothing but a simple set with a few key characteristics. Category theory is, in essence, the expression of complex ideas as simple collections of objects to unite mathematics and science as a whole.  

References

Category theory for Scientists (old version) – MIT mathematics. (n.d.). Retrieved October 24, 2022, from https://math.mit.edu/~dspivak/CT4S.pdf

Döring, A., & Isham, C. J. (1970, January 1). A Topos Foundation for theories of physics: I. Formal languages for physics. AIP Publishing. Retrieved October 24, 2022, from https://aip.scitation.org/doi/abs/10.1063/1.2883740

Guts, A. K., & Grinkevich, E. B. (1996, October 31). Toposes in general theory of relativity. arXiv.org. Retrieved October 24, 2022, from https://arxiv.org/abs/gr-qc/9610073

Lippe, E., & Ter Hofstede, A. H. M. (1996, January 1). A category theory approach to Conceptual Data Modeling. RAIRO – Theoretical Informatics and Applications – Informatique Théorique et Applications. Retrieved October 24, 2022, from http://www.numdam.org/item/ITA_1996__30_1_31_0/

Marquis, J.-P. (2019, August 29). Category theory. Stanford Encyclopedia of Philosophy. Retrieved October 24, 2022, from https://plato.stanford.edu/entries/category-theory/

 Orew – Eugenia Cheng. (n.d.). Retrieved October 25, 2022, from https://eugeniacheng.com/wp-content/uploads/2017/02/cheng-architecture.pdf

Shiebler, D., Gavranović, B., & Wilson, P. (2021, June 13). Category theory in machine learning. arXiv.org. Retrieved October 24, 2022, from https://arxiv.org/abs/2106.07032

Tran, C. S., Nicolau, D., Nayak, R., & Verhoeven, P. (2021, July 1). Modeling credit risk: A category theory perspective. MDPI. Retrieved October 24, 2022, from https://www.mdpi.com/1911-8074/14/7/298

Tuyéras, R. (2018, August 1). Category theory for genetics II: Genotype, phenotype and haplotype. arXiv.org. Retrieved October 24, 2022, from https://arxiv.org/abs/1805.07004v2

Tuyéras, R. (2020, April 4). Category theory for Genetics I: Mutations and sequence alignments. arXiv.org. Retrieved October 24, 2022, from https://arxiv.org/abs/1805.07002

 What is category theory anyway? RSS. (n.d.). Retrieved October 24, 2022, from https://www.math3ma.com/blog/what-is-category-theory-anyway