Braess’ Paradox: The Counter-Intuition of Optimization
Written by: Advaitaa Nagulapalli
Time is incredibly valuable, so it’s natural that speed and efficiency are the first priority of many, especially when it comes to arriving at a destination on time. Traffic is a major problem for everyone, so to try to reduce jams, it seems natural to add a road or two to allow for smoother car flow, right? Actually, it seems that the opposite might happen: all roads’ travel time may increase with the addition of a road.
Introducing Braess’ Paradox
Braess’ paradox is the concept of the collective increase of car travel time with the addition of a road. Fig. 1 illustrates the traffic model of Braess’ paradox. The model includes 4 different roads connected into 2 consecutive parts. There is a road connecting points 1 to 2, 2 to 4, 1 to 3, and 3 to 4.
Figure 1
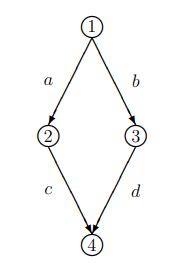
Braess’ Paradox Model 1
Source: University of Massachusetts
Now, assume that road segments a and d are narrow roads, so the speed of travel depends on the number of drivers (D) and is defined as the number of travelers divided by 100 (# of travelers driving at a time for travel time to equal 1 minute). Road segments b and c are highways that take 25 minutes to travel consistently, as highways have a speed limit and are designed for a faster flow of vehicles. Thus, the time to travel each route (1-2-4 or 1-3-4) is
(D/100) minutes + 25 minutes
This concept relies on each driver taking the path most favorable to them. If either route were shorter, any reasonable driver would take it instead, but because both the routes take the same time to travel, after a period of settling, it can be assumed that roughly an equal number of drivers will take each route. In this hypothetical scenario, it can be assumed there are 2,000 drivers attempting to travel from point 1 to point 4, so about 1,000 cars drive through each route. By replacing D with 1,000, it can be found that while segments b and c take 25 minutes to travel (constant), a and d take 10 minutes (1,000/100 minutes) each, and so the total time of each road is 35 minutes, as one can see:
(1,000/100) minutes + 25 minutes
The Effect of Adding a Road
Now, the city has constructed an additional road e from point 2 to 3 which takes a consistent minute to travel, as seen in fig. 2. If the people continue taking their original route but those who take 1-2-4 optimize their route to 1-2-3-4 (so D is still equal to 1,000), taking this shortcut takes about 21 minutes through this equation
(1,000/100) minutes + 1 minutes + (1,000/100) minutes
21 minutes seems significantly less than 25 minutes, so everyone, as sound, logical thinkers who want the fastest, most optimal route, will decide to take this route.
Figure 2
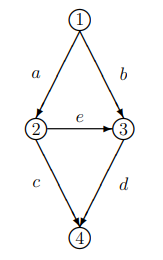
Addition of a Road in Braess’ Paradox
Source: University of Massachusetts
Due to this desire for individual optimization, in the end, all cars decide to take this route from point 1 to point 4 to decrease their travel time. Because 2,000 cars now take this route (D=2,000), the travel time of the shortcut increases to 41 minutes through this equation:
(2,000/100) minutes + 1 minutes + (2,000/100) minutes
Say one car realized the ironic inefficiency of traveling the shortcut and wanted to travel one of the regular routes (1-2-4, 1-3-4). The problem, however, lies in the fact that the travel times for these routes have also increased significantly due to the existence of road e, as the number of drivers on road segments with driver-dependent speeds (which can be found in all 3 possible routes from 1 to 4) now take 45 minutes to travel, as seen in:
(2,000/100) minutes + 25 minutes
Thus, we can see from how the time to travel each road increased from 35 minutes to 45 minutes and 41 minutes with the shortest route that the addition of road e actually increased traffic and travel time, decreasing efficiency.
The addition of a road does not necessarily result in the decrease of travel time, but can increase it for everyone. There are many instances in the real world where closing a shortcut road like road e in-fact does decrease the traffic for everyone. This phenomenon has not only been observed in car traffic, but in electron flow in electrical systems as well, and can be modeled using a spring and string model. Braess’ paradox explores the effects of system optimization and user favorability, and how its effects may sometimes seem counterintuitive due to logical reasoning and the desire for efficiency.
References and Sources
Boyd, A. (n.d.). Braess’s paradox. The Engines of Our Ingenuity. https://engines.egr.uh.edu/episode/2814
Muller, D. (2025, June 30). This mechanism shrinks when pulled. YouTube. https://www.youtube.com/watch?v=-QTkPfq7w1A&t=556s
Nagurney, A. (2020). The Braess Paradox. https://supernet.isenberg.umass.edu/articles/braess-encyc.pdf