Written by: Jaylin Park

Introduction

“Beautiful” is probably one of the first words that comes to mind when one is asked to describe nature. Flowers, leaves, crystals, snowflakes, even shells, are all considered beautiful. People often put these as their screen backgrounds for a reason. Interestingly enough, if you look closely, you will notice that all of these have geometry embedded in how they are shaped. However, does this geometry exist only for aesthetic purposes? Rather, maybe it has a purpose that goes deeper than just visuals. 

Geometry’s Role in Nature

Geometry is almost everywhere in nature, from the movement of animals to the spiral of a seashell. But nature has this geometry because it reflects mathematical principles involved in physical and biological processes. The interactions that occur within nature are often efficient, stable, and repeatable. Geometry is a perfect representation of all of these traits. It serves as the model for the patterns that emerge from nature’s interactions.

Examples of Geometry in Nature

One of the most important traits that geometry helps take place in nature is efficiency. The Honeycomb Conjecture supports the claim that hexagons are the optimal shapes to use when dividing a flat surface into equal sized areas with a minimal amount of material. Therefore, the hexagonal shape of honeycombs allows for the bees to store the greatest amount of honey while using the least amount of wax possible. Because hexagons are the most efficient polygon to tessellate and store honey in, these are the perfect shapes for bees to use when building honeycombs to store their honey. 

Another example of geometry providing efficiency is in the formation of petals and leaves in plants. The arrangement of petals on a flower and leaves around a stem follows the Golden Ratio. This optimizes exposure to sunlight and space, because the angle that each new leaf or petal is positioned at is at the golden angle (which is about 137.5 degrees) which allows for maximum sunlight capture. The rotation of a leaf around the center for when a plant has spirals tends to be made with two Fibonacci numbers which approach the Golden Ratio. The Fibonacci numbers are a set of numbers that start with 1 and 2 and the following are the sums of the two previous numbers in the set. The two Fibonacci numbers for the rotation of the plant leaves form a fraction. For example, ½, ⅗, and ⅝. As this pattern continues, the value of the angle between the leaves approaches the Golden Ratio’s value of about 1.618.

Figure 1

The arrangement of the petals of this rose follows the golden ratio spiral.

Source: [Picsart]

Trees are also plants that are designed with shapes for efficiency, but they benefit from special geometric shapes called fractals. Fractals appear in many other things such as pinecones, rivers, and succulents. These shapes are able to maximize surface area and fluid flow. Trees have branches that have more branches growing out of them. This fractal design of the branches maximizes their exposure to sunshine and ensures that water and nutrients reach every cell with minimal energy loss. The reason for this is because fractals branching structures and self-similarity allow for a large surface area to be packed into a small volume. 

Stability and strength are traits that geometry also represents well. Spirals are a shape that provide stability. Seashells grow in logarithmic spirals which allows them to grow in size without having to change shape. More specifically, if the angle between the tangent to the curve at a point on the outside of the spiral and a radial line stays constant, the shell grows in a way that keeps the shape of the spiral even as it increases in size. This can be seen in the figure below where the radial line is the red line from O to the shorter red line a that is tangent to the shell. 

Figure 2

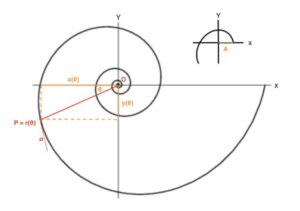
A visualization of the logarithmic spiral of a seashell.

Source: [McGill]

This helps the animal inside grow in a compact manner which is crucial to its survival, especially in underwater currents. The spiral shape also provides strength and protection to the animal inside as it distributes pressure to make the shell more resistant to crushing forces. 

While the intricate geometric formations of crystals reflect the internal structures that compose them, they are often also affected by external conditions. However, most crystals do resemble the Wulff shape, which is a model of equilibrium for crystals and found by using the surface energies of the crystal faces. Surface energy is the extra energy that the atoms on the surface of a crystal possess compared to atoms on the inside of the crystal. This extra energy is from the potential that the atoms on the outside have to move, because they are not stable and surrounded by other atoms on all sides. Therefore, higher surface energy means a higher probability of change such as dissolving or growth. The Wulff shape minimizes surface energy and is therefore less likely to change under environmental stress. The symmetry and repeating patterns that are created from the arrangement of atoms in the crystals also ensure that the impact of forces applied to it are distributed evenly throughout the structure. This makes it harder to fracture. 

Finally, geometry also helps provide stability to animal movements. Both the arrangement of animal body parts and the way that their movements are formed involve geometry. The joint angles and limb lengths affect the effectiveness of animals’ gaits. Animals flex and extend their joints in an oscillatory pattern. The locomotion of animals who use their legs to move involve something called a support polygon. The animal is stable while walking if it has enough legs to create the support polygon. A support polygon is simply the shape formed by the feet that are on the ground when the animal is moving. It can be determined whether or not an animal is statically stable by forming the support polygon by creating edges between the animal’s legs then seeing if the center of mass is inside or outside the polygon.

Figure 3

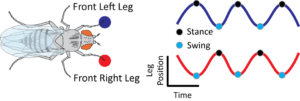
An oscillating pattern from the movement of the legs of the insect can be seen.

Source: [Wikipedia]

Conclusion

There seems to be an endless number of ways that geometry is involved in nature. Shapes and numbers like the Golden Ratio, fractals, spirals, patterns, and symmetry all appear often. These help increase the efficiency, stability, and strength of interactions that occur in the natural world. Without the geometry that is woven into nature, the world would not only lose much of its natural beauty, but also much of the plants, animals, and environment that we are surrounded by. So, the next time you look at a rose, maybe you will not just admire its satisfyingly perfect formation, but also the beautifully intricate geometry that shapes it.

References and Sources

Cole, E., Linaje-Ferrel, G., Oraichi, S., & Phung, M. (n.d.). Mathematical Models of Molluscan Shell Patterns and Morphology. McGill. Retrieved October 9, 2025, from https://bioengineering.hyperbook.mcgill.ca/mathematical-models-of-molluscan-shell-patterns-and-morphology/

Cristian. (2024, September 5). Geometry in Nature: Discovering Shapes in the World Around Us. Geometry Contest. Retrieved October 9, 2025, from https://geometrycontest.com/geometry-in-nature-discovering-shapes-in-the-world-around-us/

14 Interesting Examples of the Golden Ratio in Nature. (2025, April 15). GeeksforGeeks. Retrieved October 9, 2025, from https://www.geeksforgeeks.org/maths/14-interesting-examples-of-the-golden-ratio-in-nature/

Gunther, S. (n.d.). 9 Amazing Fractals Found in Nature. Treehugger. Retrieved October 9, 2025, from https://www.treehugger.com/amazing-fractals-found-in-nature-4868776

Nature, The Golden Ratio and Fibonacci Numbers. (n.d.). Math is Fun. Retrieved October 9, 2025, from https://www.mathsisfun.com/numbers/nature-golden-ratio-fibonacci.html

Olwan, S. (2024, November 27). Nature’s Geometry: Uncovering Glamorous Patterns and Shapes in the Wilderness. LearningMole. Retrieved October 9, 2025, from https://learningmole.com/natures-geometry-finding-shapes/

Reality Pathing. (2025, July 17). Why Do Honeybees Prefer Hexagonal Shapes for Their Honeycombs? Reality Pathing. Retrieved October 9, 2025, from https://realitypathing.com/why-do-honeybees-prefer-hexagonal-shapes-for-their-honeycombs/

Simple Science. (2025, August 23). Crystal Shapes and Their Stability Insights. Simple Science. Retrieved October 9, 2025, from https://scisimple.com/en/articles/2025-08-23-crystal-shapes-and-their-stability-insights–akyx765

Tuhin, M. (2025, May 26). The Physics of Crystal: Order at the Atomic Level. Science News Today. Retrieved October 9, 2025, from https://www.sciencenewstoday.org/the-physics-of-crystals-order-at-the-atomic-level

Wikipedia. (n.d.). Study of animal locomotion. Wikipedia. Retrieved October 9, 2025, from https://en.wikipedia.org/wiki/Study_of_animal_locomotion