Written by: Oscar Lee

        Start with any positive integer. If it’s even, divide it by 2; if it’s odd, multiply it by 3 and add 1. Keep repeating this process, and (mathematicians think) you will eventually reach the number 1. This is the Collatz Conjecture, and it is one of math’s most well-known mysteries., we will cover the history of this infamous conjecture, and how it has stumped mathematicians for nearly a century despite its implicit simplicity. 

What is the Conjecture?

        The conjecture is simply an algorithm, as stated in the introduction. Take the number 5. Since it is odd, we multiply it by 3 and add 1. 5*3+1=16. 16 is even, so we divide by 2, getting 8. 8 is also even, so dividing by 2, we get 4. 4 is even, so we divide by 2, and we get 2, which gives us 1. This “simple” algorithm always seems to return 1.  Despite this, mathematicians have completely failed to find a proof that this happens for every integer. There are two ways mathematicians could disprove the conjecture. Number one, there could be a sequence of numbers that grows to infinity. Or, number two, there exists a series of numbers that form a “loop”, effectively never returning to 1. However, the only loop that has been found is 1→ 4 → 2 → 1, which trivially satisfies the conjecture.

Early History

        The problem was proposed in 1937 by German mathematician Lothar Collatz. He reportedly discussed it with other mathematicians in Hamburg at the time, and later in Berlin, where the conjecture spread in the form of rumors among number theorists. The problem quickly gained popularity and infamy through mathematicians such as Paul Erdos, Kurt Mahler, and John von Neumann. Erdos popularized the problem by mentioning it frequently in his talks and conversations, and even offered cash prizes for progress. During this period, no major papers were written regarding the conjecture, but it became widely known in the math world. 

        The first formal publication of the problem in print was during the 1950s, where it went by a lot of names, including: “3n+ 1 problem”, “Ulam problem”, “Syracuse problem”, and “ Hailstone problem”. The name “hailstone” was popularized by its analogy with hailstones rising and falling within clouds, which looked similar to the graphs of the conjecture (See Figure 1). 

        This graph was created by having the number of times the algorithm has run on the x-axis, and the number the algorithm outputs on the y-axis. Collatz himself published a short description in 1957, but it still remained largely outside of mainstream mathematics research.

Figure 1

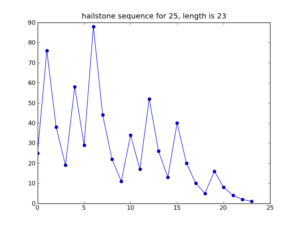
A “hailstone sequence” graph for the number 25. The “length” describes the number of iterations of the algorithm required to reach 1.

Source: Glowing Python

Modern Developments

        With the invention and development of computers, mathematicians began brute-forcing the problem, plugging large numbers into the algorithm. By the 1960s, mathematicians had tested up to the number 10 million. By the 1970s, that number was extended into the billions. In the 1970s, Conway showed that generalized Collatz-like problems approach the boundaries of conventional mathematical logic, and thus the original Collatz problem may even be undecidable”.

        By the 1980s, the problem appeared in mainstream official mathematical research, with many establishing it as a central unsolved problem in number theory. As computers continue advancing, testing also continues to improve. As of 2020, the conjecture has been verified for numbers up to 2^68.  In 2019, Terence Tao, Fields Medalist and youngest IMO medalist, made what is considered to be the most significant progress in decades, proving that almost all Collatz paths obey an averaged contraction property.

Figure 2

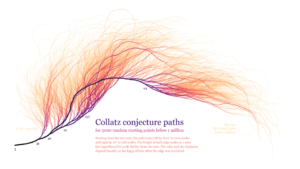
Another graph of Collatz conjecture paths, resembling coral and organic organisms.

Source: Wikipedia

Conclusion

       Whether it be its hailstone peaks, or its apparent “numerical gravity” as numbers always plummet down towards 1, or its beautiful coral patterns when graphed simultaneously, the Collatz Conjecture has proven to be one of the most elegant yet chaotic theories in the field of math. Because of its infamy, there is a $1 million+ bounty for whoever can prove the conjecture, so maybe in our lifetime, we will get to see this problem be solved, and we’ll be excited when it happens.

References and Sources

Collatz conjecture. (2020, September 9). Wikipedia. https://en.wikipedia.org/wiki/Collatz_conjecture

Honner, P. (2020, September 22). The Simple Math Problem We Still Can’t Solve. Quanta Magazine. https://www.quantamagazine.org/why-mathematicians-still-cant-solve-the-collatz-conjecture-20200922/

The Collatz conjecture. (2021). Blogspot.com. https://glowingpython.blogspot.com/2011/06/collatz-conjecture.html 

Muller, D. (2021, July 30). The Simplest Math Problem No One Can Solve – Collatz Conjecture. Www.youtube.com. https://www.youtube.com/watch?v=094y1Z2wpJg 

‌