Written by: Meghna Manoj

“There is geometry in the humming of the strings, there is music in the spacing of the spheres.”

–Pythagoras

Introduction

Math is deeply intertwined with music, from the most basic to complicated concepts, like keys, ‘beats’, harmonies, and intervals. Ken Alexander, a professor of math at USC Dornsife, is quoted in an article by Margaret Crable, “What’s written on a page of music is just a sequence of pitches and how long you hold each pitch. You have to see that, underneath, there are themes, flows, and a cadence in the music. There are all kinds of patterns that you have to identify…In math, a lot of great insights and breakthroughs come about when people see how different parts of mathematics are actually related to each other. Pattern recognition is a very central aspect,” (Crable, 2024). Math is the study of patterns and structure, acting as a foundation for the ideas used to compose music. 

Numbers and Musicians

Bach, considered one of the greatest classical composers, incorporates the number 14 in many of his pieces, (Bach’s name in numerology, the assignment of letters in the English alphabet to numbers), like the 14 canons in the Goldberg Variations. There’s also the motif of B♭-A-C-B♮, BACH in German notation, in the final unfinished fugue of “The Art of Fugue”. Bach utilized many mathematical concepts in his works. For example, in Musikalisches Opfer, a collection improvised on themes played by King Frederick the Great of Prussia for him, he created the “Crab Canon”. In this canon, Bach rewrites the notative beginning, including the key signature (sharps and flats) and time signature (number of beats per measure and how many beats each note gets) of the song at the end of the piece, upside-down. The canon can be played forwards or backwards, and both ways at the same time (playing in retrograde), displaying symmetry in music. It can also be written on a 1-sided transparent Möbius strip, a piece of paper that twists, loops and comes back together to where it began, and when played, the retrograde plays at the same time as the original piece, and it comes back to the beginning eventually; Bach used a mathematical concept yet to be discovered. 

Figure 1

Description: Example of a one-sided, transparent film Möbius strip with the “Crab Canon”

Source: https://veritasjournal.org/2022/12/15/bachs-favorite-number/

220 years later, in 1967, John Coltrane, a renowned composer, jazz saxophonist, and bandleader, created the “Circle of Tones”, illustrating the connection between music notes and tonal relationships through its depiction of the 12 semitones of the chromatic scale. It’s known for its connection to musical geometry, encouraging numerous studies and essays, and is thought to have been inspired by the same geometric theories that motivated Einstein’s quantum theory, simultaneously connecting music, math, and physics (Baron, 2024). 

Figure 2

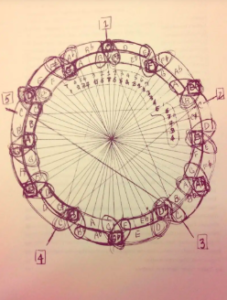
Description: Coltrane’s original “Circle of Tones”

Source: https://mymodernmet.com/the-coltrane-circle-mathematics-and-music/

Mathematical Concepts

When a note is played on a string fixed at both ends, it creates a sine wave that oscillates between the two points. The harmonics of the sine wave are overtones, accompanying waves that make a complex sound with varied tone quality – timbre – and get progressively smaller in wavelength, so ½, then ⅓, ¼, and so on (creating the harmonic series). Instruments, including the human voice, can manipulate these kinds of harmonic waves to create different sounds. Additionally, musicians split sound waves into 12 ratios, as opposed to lengths, so mathematicians found the 12th root of 2 to understand the spacing of the notes in an octave, creating keys. After this calculation became possible, Bach wrote the Well-Tempered Clavier, a collection of 48 preludes and fugues in every key. 

Figure 3

Description: The distribution of octaves by frequency

Source: By Basavarajtalwar – Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=15526047

Conclusion

Composers like Bach and Coltrane, among many others, used mathematical patterns and concepts in their compositions, and today’s mathematicians and musicians are beginning to see the connections. Without these connections, many parts of music and theory might’ve never been created, like the octave, harmonics, and intervals. Math and music aren’t different languages, but rather, versions of the same song.

References and Sources

American Mathematical Society. (2019). Mathematics and Music. American Mathematical Society. https://www.ams.org/publicoutreach/math-and-music

Baron, E. (2024, December 27). John Coltrane’s “Circle of Tones” Illustration Beautifully Visualizes the Connections Between Mathematics and Music. My Modern Met. https://mymodernmet.com/the-coltrane-circle-mathematics-and-music/

Canon perpetuus from Musikalisches Opfer – Bach. (2021). Netherlands Bach Society. https://www.bachvereniging.nl/en/bwv/bwv-1079-11

Crable, M. (2023, April 27). Musical numbers: Math and music nurture a deep and complex relationship. USC Dornsife. https://dornsife.usc.edu/news/stories/relationship-between-music-and-math/

Rubio, C. (2022, December 15). Bach’s Favorite Number. Veritas Journal. https://veritasjournal.org/2022/12/15/bachs-favorite-number/

Talwar, B. (2024). Distribution of octaves by frequency [Image]. In Wikipedia. https://commons.wikimedia.org/w/index.php?curid=15526047