Written By: Shihan Cheng

Poker is a game of incomplete information. Players must make decisions with uncertainty, ultimately relying on probabilistic outcomes to determine the winner of a round. Unlike popular games such as chess or Go, Poker has the element of hidden cards and not knowing what cards will show up on the table, making it extremely viable to research in fields such as artificial intelligence (AI) and game theory. Game Theory Optimal (GTO) Poker refers to a methodology of playing Poker with a Nash equilibrium strategy so that no opposing player can deviate their playing style to improve their expected value of winnings. GTO Poker consists of choosing to bet (putting more money at stake), call (matching someone else’s bet), and fold (giving up a hand), at certain frequencies such that the opposition cannot capitalize and profit from counter-strategies in the long run.

First we introduce the basic rules of Poker. Each player attempts to make the best possible five-card hand, which has a hierarchy, given their two hole-cards, which are personal to them and not shared by anybody, along with the five community cards, which all players share on the table. There exists four betting rounds: pre-flop, before any of the community cards are shown, flop, after the first three community cards are shown, turn, after the fourth community card is shown, and river, after the fifth and final community card is shown. Players attempt to maximize their profits if they have the optimal five-card hand, and minimize their losses if they do not. 

GTO Poker is rooted in non-cooperative game theory, which was pioneered by John von Neumann and Oskar Morgenstern in Theory of Games and Economic Behavior, published in 1944. In a two-player zero-sum game, which means that every positive to one player directly yields a negative to the other, a Nash equilibrium is the pair of strategies where each player’s choice is the optimal response to the other’s. Mathematically, let S1 and S2 denote the set of possible strategies, or actions, that player 1 and player 2 has, respectively, and u1(s1, s2) be the expected utility, or winnings, or player 1 given strategy pair (s1, s2) for some strategy s1 in S1 and s2 in S2. Then a Nash Equilibrium must satisfy that

u1(s1∗, s2∗) ≥ u1(s1, s2∗), u2(s1∗, s2∗) ≥ u2(s1∗, s2)

for all possible s1 and s2. Note that s1∗ and s2∗, which are deviations in strategy, often include mixed strategies, where certain actions are played at specific frequencies. This Nash equilibrium ensures that each player’s expected win rate is maximized when playing against perfectly reasonable play.

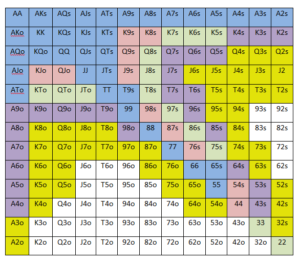Figure 1: A GTO Chart demonstrating the specific frequencies of actions that a player should have pre-flop in a certain position.

Completely solving GTO strategies for Poker is extremely computationally challenging, as there exists around 10161 possible states, more than the number of atoms in the observable universe. Due to this enormous number, researchers often use abstraction techniques in order to reduce this number, such as grouping similar hands and similar situations into clusters. They utilize counterfactual regret minimization (CFR) algorithms. CFR essentially uses the question “If I could go back in time and play differently, how much better off would I have been?” The “how much better off ” in the above hypothetical scenario is defined as regret. Through millions of practice games and iterations, CFR minimizes this regret, ultimately converging to a Nash Equilibrium strategy profile.

While a GTO Poker strategy is theoretically unexploitable, it’s designed to minimize one’s losses against good players instead of maximizing wins against suboptimal opponents. Many professional players adopt the concept of a GTO baseline to avoid being exploited, but they also adjust their strategy to exploit their opponent when their opponent deviates from GTO. This dynamic balance between equilibrium and exploitation is an active area of study in poker trading software and multi-agent reinforcement learning.

GTO formalizes optimal Poker play using ideas from game theory and algorithmic computation. It has not only advanced the beautiful game of Poker, but it has calso ontributed to the rapidly growing field of AI and decision-making. Applications include operations management for large corporations, resource allocation, path planning for robotics, and so much more. Researchers continuously study GTO, both refining human strategy in Poker games, but also developing better strategic reasoning in imperfect-information games.

References

1. Cornell University INFO 2040 Course Blog. Game theory optimal (gto) texas holdem poker theory, November 2021. Accessed: 2025-09-13.
2. Jingyu Li. Exploitability and game theory optimal play in poker. Undergraduate seminar paper, course 18.204 (discrete mathematics), Massachusetts Institute of Technology, May 2018. Accessed: 2025-09-13.
3. John von Neumann and Oskar Morgenstern. Theory of Games and Economic Behavior. Princeton University Press, Princeton, NJ, 1944.
4. William Poundstone and The Editors of Encyclopaedia Britannica. John von neumann — biography, accomplishments, inventions, & facts, July 2025. Accessed: 2025-09-13.