Written by: Advaitaa Nagulapalli 

Introduction

Take a second to ask yourself: what is the shortest distance between two points? Many will instinctively say it is a line. This statement is quite reasonable, especially in certain math and geometry. However, when outside elements such as gravity and acceleration are introduced, this statement no longer holds true. The realization that the path of least distance is not always the path of least time reveals new possibilities in the fields of motion and optimization.

Setting up the Scenario

What do you think is the fastest path from a point A to a lower point B (not directly below) with gravity as the only moving force? While a line is certainly the shortest in distance, as illustrated by the blue line in Fig. 1, it is not the fastest, due to the steady acceleration from beginning to end. Now, let’s consider another path, one that has a steep slope at the beginning and transitions to a shallow slope until point B. This path, the grey path labeled 2 in Fig. 1 is certainly longer, but due to the increased acceleration (as gravity is acting upon the object) at the steep slope, the particle that rolls down this path will reach point B faster. 

Figure 1

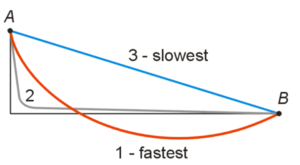
A Representation of the Brachistochrone Curve: Modeling Paths from Point A to Point B

Source: MathOnWeb

When considering acceleration and the length, finding the perfect combination results in the fastest route from point A to point B is called the Brachistochrone Problem. The solution to this Brachistochrone Problem is the Brachistochrone Curve, the red curve in Fig. 1.

What is the Brachistochrone?

The term “brachistochrone” comes from the ancient Greek words “brákhistos,” which means “shortest,” and “khrónos,” which means “time.” Devised by Johann Bernoulli in 1696, the Brachistochrome Curve is the path of steepest descent when acted upon by gravity that allows for the travel from a higher point A to a lower point B in the least amount of time. As previously explained, the Brachistochrone Curve is a combination between the shortest distance and fastest route when considering gravity and acceleration. 

Snell’s Law of Light Refraction

Snell’s Law states that light will always take the fastest path through a medium. If there is a sudden change in medium, light will be refracted in the way that will allow it to take the least time to travel through the medium. 

Figure 2

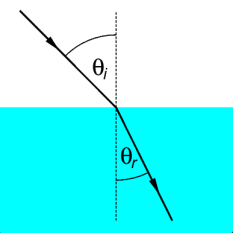
Model of Light Refraction as per Snell’s Law

Source: University of Massachusetts

Fig. 2 displays the angle of light refraction when light travels from a medium in which it can travel faster to a medium which slows in down, like from air to water. Since light always takes the fastest route and light refracting and changing speed through denser to less dense mediums is similar to the acceleration of a falling object. Bernoulli uses Snell’s law to find the solution to the Brachistochrone Problem. As one models the path of light using Snell’s Law of refraction through a series of mediums from most dense to least dense, as seen in Fig. 3, one can see a curve-like shape slowly forming from the connected line segments. 

Figure 3

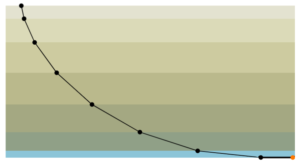
Light’s Path Through a Series of Mediums Creating the Brachistochrone

Source: Wolfram Demonstrations

As the number of mediums reaches infinity, the shape becomes the path known to be the magical Brachistochrone Curve.

The Brachistochrone Curve is a Cycloid

To begin to understand this Brachistochrone Curve formed by Snell’s Law, one must understand that it is also a cycloid, which is a type of roulette. What is roulette? When an object rolls, it is moving in respect to another object and stays in contact with it in such a way that all contact points have immediate velocities of zero, so the said object does not slide while rolling. If a point is marked on a rolling item, the path it traces is called a “roulette.” The roulette that is formed by a rolling circle along a line is called a “trochoid,” which can be “curtate” if the point is within the circle, or “prolate” if it is outside the circle. When the point is on the circumference of the circle, the roulette formed is called a “cycloid.” In Fig. 4, the bottom roulette is curtate, the top roulette is prolate, and the middle roulette is a cycloid.

Figure 4

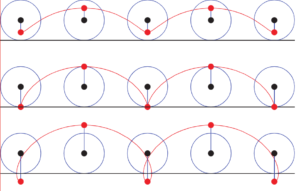
Modeling Types of Roulettes

Source: Wolfram MathWorld

This cycloid satisfies Snell’s Law, and is yet another way to create a Brachistochrone curve. 

Conclusion

One can see that when considering the travel of a particle from a higher point A to a point B that is not directly underneath when acted upon by gravity, the fastest route is not a line. Derived from Snell’s Law by Bernoilli, and able to be constructed from a cycloid, the Brachistochrone Curve is the perfect balance between acceleration and length, so a particle which rolls down this path will reach point B at the fastest possible rate: not the path of least distance but the path of least time.

References and Sources

CuriousWalk. (2021). Cycloid: Curve of Fastest Descent. YouTube. https://www.youtube.com/watch?v=-H7CzIGcQk4&t=87s

Oregon State University. (n.d.). Understanding the Nature of Light. https://sites.science.oregonstate.edu/~giebultt/COURSES/ph332/Chapter01.pdf

Vsause. (2017). The Brachistochrone. YouTube. https://www.youtube.com/watch?v=skvnj67YGmw&t=329s

Weisstein, E. (n.d.). Trochoid. Wolfram MathWorld. https://mathworld.wolfram.com/Trochoid.html