Muon g-2: Breaking the Standard Model

On April 7, 2021, the Fermi National Accelerator Laboratory (FNAL) announced the groundbreaking first results of the Muon g-2 experiment. This long-awaited experiment looked to measure the magnetic moment of the muon to an immense precision, running from 2017 into late 2020, and further data analysis of these tests taking another year after that.

The magnetic moment of the muon had been predicted to a very precise value by the Standard Model \((\)\(\text{g-factor}: 2.00233183620(86)\)\()\). Different runs of the Muon g-2 experiment were aimed at confirming an experimental contradiction to the Standard Model predictions. This goal came to fruition as the results of Run-1 were sifted through, and it yielded a contrasting \(\text{g-factor}: 2.00233184122(82)\).

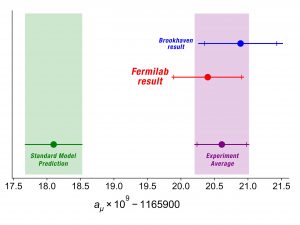
The new Fermilab Muon g-factor results helped confirm initial Brookhaven National Laboratory results that introduced the potential of Standard Model Contradictions in 2001 | Source: FNAL

But why would physicists want the Standard Model to be wrong?

The Standard Model of Particle Physics (or simply the Standard Model; SM) is widely considered the most successful scientific theory based on the enormous amounts of testing and experimental support. This model describes the elementary particles of the universe, with both matter and forces being represented as fundamentally quantum in nature. That is to say, the behaviors of the smallest, most basic building blocks of the universe are defined as being probabilistic. This trailblazing notion indicated that any attempt to observe a fundamental particle to gather more data would change the nature of the particle and, therefore, the results of the experiment. This innately results in challenges when trying to collect data about these elementary particles.

However, certain theoretical pieces are missing in the Standard Model, indicating an inherent incompleteness and a necessity for new models to be proposed and tested. Some major flaws with the current Standard Model include:

• It does not consider gravity (one of the four fundamental forces, alongside electromagnetism and the nuclear forces).
• It currently cannot predict why gravity is so much weaker than the other fundamental forces at a quantum scale.
• It also has no concrete explanation for the nature of either dark matter or dark energy, of which the majority of the universe is made of.

In search of support for new models, the experimental side of the physics community conducts tests to measure certain characteristics of the particles on the SM, as well as to search for potential new particles that could open up the way for new advancements. These tests are operated mostly through the use of particle accelerators, where two subatomic particles collide with one another, and the resulting energy signatures are studied and analyzed using data science techniques, in search of any irregularity that contradicts the SM.

Simultaneously, the theoretical side of physicists searches for mathematical ways to explain the gaps in SM, introducing potential descriptions of said phenomenon. Then based on experimental results, the theories can be assessed and revised repeatedly, with the hopes of finding a mathematical model that could better explain the missing areas on the SM.

The Standard Model predicts certain characteristics of the fundamental particles. These characteristics include the following:

• the estimated mass of particles
• the direction of angular momentum (spin) of particles
• the positive or negative electric charge of particles
• coupling to the weak nuclear interaction; the “weak charge” of particles
• the “color charge” of particles under the interaction of the strong nuclear force in atomic nuclei

In Newtonian and Einstein’s gravity, as well as Maxwell’s electromagnetism, these “charges” create fields surrounding based on their respective position and momentum. However, as dictated by Heisenberg’s Uncertainty Principle, it is impossible to measure both position and momentum of a subatomic particle because of its probabilistic behavior. Therefore, quantum fields must also be considered to be fundamentally different in nature from classical fields.

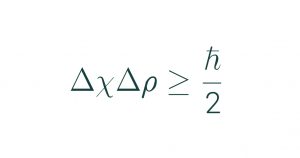
The Heisenberg Uncertainty Principle, named after German physicist Werner Heisenberg, mathematically describes the probabilistic impossibility to measure both displacement \((\Delta x)\) and momentum \((\Delta p)\) of a subatomic particle. Oftentimes, the principle is written using the respective uncertainties of these values \((\sigma _{x,p})\). This contribution redefined the field of Quantum Mechanics, with the prevalence of non-commuting operators taking a major role in modern physics, such as Quantum Field Theory | Source: Harvard Review

This opened up the branch of theoretical physics dubbed Quantum Field Theory (QFT). QFT has various (although equivalent) formulations that individually have innate complications. However, the existence of quantized fields that exist without the stimulation of quantized “charged” particles, indicates that certain measurements made for the characteristics of SM particles must be re-evaluated.

One of these characteristics is the spin magnetic-moment of the muon (μ), one of the six leptons of the Standard Model, which essentially behaves as an exponentially heavier version of a more commonly known particle, the electron (e). The magnetic moment describes an innate attribute of particles relating spin to interaction with the electric charge.

Initial predictions of the muon magnetic moment were made by Paul Dirac, hoping to generalize quantum mechanics to fit the complications posed by Einstein’s theory of special relativity. This prediction suggested that the classical prediction of the spin magnetic moment, shorthanded as g, would have to have a multiplicative factor applied to it. This implied that g would subsequently have a value exactly equal to 2. However, because of the differences QFT brought to the Standard Model, scientists have altered the value of g to be slightly greater than 2. Therefore, the value of “g-2” indicates measuring the effects on the muon’s g that Dirac did not account for.

Because of the discrepancy between FNAL’s Muon g-2 result and the Standard Model prediction for the g-factor, there exists a reasonable belief that other forces not labeled on the SM could be influencing the muon’s behavior. Currently, Run-2 and Run-3 of the FNAL Muon g-2 experiment are completed with data still being analyzed to check the initial Run-1 results. Run-4 (the final scheduled run of the electromagnet) is ongoing, with a stream of muons being directed from Fermilab’s accelerators into the magnet to gather more results.

Only through further analysis can the anomalous spin magnetic moment be confirmed, eventually proposing new Standard Model alternatives based on these unknown interfering forces.