Calculating the Strong Force: Lattice QCD

As of August 2021, a team of postdoctoral researchers at Columbia University have successfully implemented NVIDIA’s CUDA cores to be used as a graphical computational source for Lattice Quantum Chromodynamics (LQCD). Unlike the initial stages of LQCD, this QCD on CUDA (QUDA) method of computational analysis could make use of the parallelism found in GPU architecture, allowing for faster computational speeds than with classic CPU supercomputers.

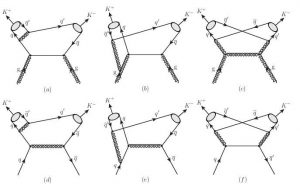
A perturbative approach of Quantum Chromodynamics can be depicted using various quark-gluon vertices in Feynman Diagrams. These diagrams show Kaon pair production methods | Source: Thomas Jefferson National Laboratory

Perturbative and Non-Perturbative QCD

Like most Quantum Field Theories (QFTs), there are various approaches to solving for the interactions of Quantum Chromodynamics. There exist two major categories of solution methods: perturbative and non-perturbative. The former takes an analytical approach to quantize the Strong Force, whether it be through a Canonical Quantization formulation or a Feynman Path Integral formulation, these perturbative methods focus on mathematical manipulation to generalize Strong Force interactions. Unlike its electromagnetic counterpart Quantum Electrodynamics (QED), the color-charged quarks \( (\text{u, d, c, s, t, b})\) cannot be observed in isolation but rather are confined within the bounds of a three-quark hadron. This complicates the process of understanding quark and gluon \((\text{g})\) interactions on their own.

Contrastingly, non-perturbative methods use computational simulations to approximate the behavior of the particles, avoiding some of the analytically difficult (and at times, unsolvable) mathematics.

The excited behavior of the gluon field surrounding quarks within a hadron can be approximated using Lattice Quantum Chromodynamics. This allows for better visualization of Strong Force interactions, compared to standard quark, gluon flux-tube diagrams | Source: BNL

Lattice QCD is a non-perturbative method for calculating approximations for the interactions between quarks and gluons within the hadrons they form, simulating these relationships rather than analytically solving for QCD. This method looks to simulate an infinitely expansive lattice of mathematical objects and then places quarks and gluons within the lattice to observe how they would interact based on experimentally derived masses, charges, spins, and energies. However, forming an infinitely expansive lattice is not currently computationally possible, resulting in physicists slowly attempting to increase the size of this lattice based on computing advancements in the field.

First developed at the Department of Energy’s (DoE) Oak Ridge National Laboratory, LQCD was used to approximate certain measurements of the quarks found within hadrons, by running simulations on its Summit Supercomputer. The results from the simulations used at Oak Ridge National Laboratory were used in subsequent high-energy collision experiments taking place at Thomas Jefferson National Laboratory and Brookhaven National Laboratory. These approximations could be used to approximate the results/characteristics of certain collisions within a particle accelerator, allowing for more precise measurements to be taken from the experiments. For example, the spin-magnetic moment of the muon \((\mu )\) was measured to have a g-factor of greater than 2 using Lattice QCD, resulting in breakthroughs during Fermi National Accelerator Laboratory’s Muon g-2 experiment in early 2021.

Following the immense success of LQCD approximation, many incremental advancements were made in developing the simulated algorithmic lattice on a variety of supercomputing systems. However, the innate drawbacks of classical computing continued to plague these simulations, as the size of the virtual lattice could only be extended to a certain extent.

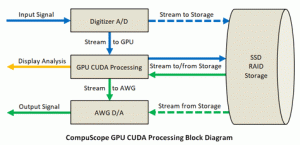
The CUDA architecture, initially developed by NVIDIA, allows for parallel processing, increasing the efficiency of data flow. Note that multiple data paths can be taken from the SSD RAID Storage, resulting in a more simultaneous process during computation| Source: NVIDIA

CPU vs. GPU Processing Speed

Central Processing Units (CPUs) and Graphical Processing Units (GPUs) both operate in a similar fashion, being formed of numerous superconductors and Boolean circuits to allow for computation. However, while CPUs have an innate advantage in the variety of tasks they can be applied to, GPUs have the advantage of running in a more simple, parallel threaded formation. This allows for significantly faster clock-speeds for modern GPUs as opposed to modern CPUs, but they can only be applied to very specific computational tasks that allow for such circuit architecture.

In June 2007, a graphics card developer NVIDIA licensed their CUDA cores: a GPU system that runs multiple CPU-style cards in parallel to one another, resulting in exponentially faster graphical systems. For many years these CUDA cores seemed to only pose benefits for certain instances on a computer, such as in running 4k video or displaying graphically intense video game output. However, as the popularity grew for the CUDA cores, simulation developers in various fields (specifically in finance, climate science, molecular modeling, condensed-matter physics, and high-energy physics) began attempting to optimize these cores for their specific needs.

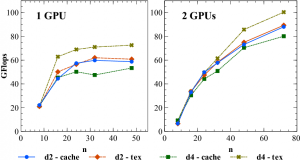
The performance of singular GPU Lattice QCD, and multiple core CUDA GPU processing. All four subsets of data storage reaches ~25% boost in Gigaflops (1 billion floating point operations per second) | Source: Department of Energy

QCD on CUDA (QUDA)

In January 2021, after noticing these optimized improvements in CUDA usage, the Department of Energy (DoE) requested a group of Columbia University researchers to attempt and apply NVIDIA’s graphical libraries to the task of simulating LQCD interactions. Headed by Bálint Joó, the team sought to use the processing speeds of CUDA cores to their benefit, and they were eventually being able to improve the accuracy of these computational approximations. After months of optimization and algorithmic advancements, the QUDA library for QCD on CUDA GPUs was made public, allowing for a variety of simulated interactions to a greater degree of accuracy.

Researchers, as sponsored by the DoE, from various national laboratories are tasked with testing this efficiency using a variety of advanced algorithms and Monte Carlo simulations. Further developments in QUDA efficiency and accuracy are perpetuated and compared against other perturbative methods of QCD, working towards a computationally sound approximation for these Strong Force interactions.