Written by: Gautham Anne

While watching boats travel by or a duck on a pond, one might wonder how the astonishing wake patterns emerge, such as the ones depicted in figure 1. One might also note that the wake patterns, regardless of whether it is being produced by a duck or even a cruise ship, all seem to have a similar shape. The famous physicist Lord Kelvin noticed an interesting fact about the wakes. Using rigorous mathematics, he determined in 1887 that the angle theta (Kelvin angle) that the wake fans out is always the same, regardless of the object and its speed, is approximately 19.47 degrees. In 1984, Frank S. Crawford, a professor of physics at the University of California at Berkeley, found theta using only elementary mathematics — specifically geometry and trigonometry. This article will attempt to present this solution as well as some controversies regarding the Kelvin angle.

Figure 1

Source: Google

Key Concepts and Vocabulary
In order to derive theta, first, one must learn the essential concepts and vocabulary in order to do so. There are two types of waves in a wake: transverse waves and divergent waves, as depicted in figure 2. However, the divergent waves are of more interest, since they are directly related to theta.

Figure 2

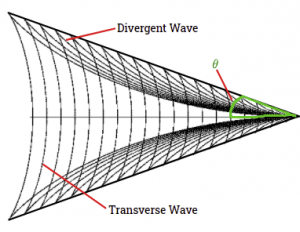
While light and sound waves propagate with the same velocity, 3 * 10^8 and 348 m/s respectively, the velocity of water waves depends on their wavelength. That is, the longer the wave, the faster it propagates. This is the fundamental reason why water wakes differ from other phenomena, such as a Mach cone, which is the pressure wave produced by bodies moving faster than the speed of sound.
On what factors do the velocity of the waves depend upon? Certainly, the wavelength lambda, the depth of the water H, surface tension sigma, the gravitational force g, and the density of water rho are all factors. However, it can be assumed that the water is sufficiently deep enough to not be a factor and since the surface tension only affects short waves, it is negligible.
The phase velocity is the velocity of the individual wave crests. Its equation is v_phase = sqrt(g*lambda/2pi). The group velocity is the velocity of the overall shape of the wake. From the expression of group velocity and the given expression of phase velocity, it can be determined that v_g = v_phase / 2, that is, the group velocity is ½ of the phase velocity. Using this relation, and the fact that water waves disperse, a geometric representation of the wake can be generated, such as the one in figure 3.

Figure 3

Geometric representation of a water wake, showing the individual propagating waves. The red dots represent the phase velocity and the shape of the wake. Boat located at point B.
Source: University of Hannover in Germany

Derivation of theta

If point B is the location of the object traveling across the body of water, then multiple constructions can be formed with point A representing the epicenter of all waves emitted from it, relative to point B. This is shown in figure 4, where each circle from point A represents a wave moving at phase velocities of 10, 20, 30 … 99.99 percent the speed of the object. Constructing tangent lines to each individual wave, joining them with point A, and representing where the waves are when the boat is at point B with the red dots as indicated in the figure, the sequence of red dots forms a circle with radius AB/4.

Figure 4

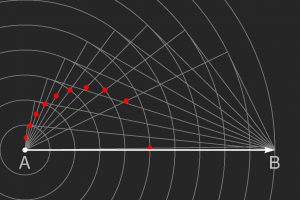
Source: University of Hannover in Germany

Constructing a tangent line to the red circle, as shown in figure 5, yields a right triangle with the side opposite to theta with length x, and the side along AB with length 3x. Using trigonometry, it can be shown that sin(theta) = x/3x = ⅓ => arcsin(⅓) = theta = 19.47 degrees.

Figure 5

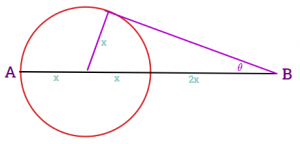
The Kelvin Wake Controversy

While looking at Google Earth images of ships, two French physicists Marc Rabaud and Frédéric Moisy, saw that some of the wake angles were not 19.47 degrees, that is, they did not conform to the prediction that Lord Kelvin made in 1887. Before their discovery, narrower wakes have been spotted, but scholars stated that they were due to unique circumstances such as shallow waters, turbulence, and more.
Raubad and Moisy discovered that even without all of these circumstances, some ships still had smaller wake angles. They created new mathematical models to describe the narrower wakes through analyzing the images and making measurements of the hull lengths, wake angles, the velocities, and assuming that an object of length B cannot produce wavelengths greater than B. Their numerical simulations seem to suggest that at higher speeds, boats would produce smaller wake angles. Figure 6 shows the effect of higher speeds on the wake angle alpha. Fr represents the Froude number, which directly varies with respect to the velocity of the object.

Figure 6

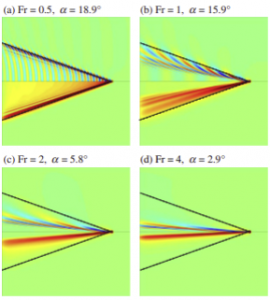
Source: Physical Review Letters; Ship Wakes: Kelvin or Mach Angle?

Professor Simen Ellingsen of the Norwegian University of Science and Technology recently found the solution to the controversy. He proposed that the reason why boat wakes may be narrower than 19.7 degrees is due to a phenomenon called shear flow. Shear flow occurs when there are different currents in different layers of water, and Kelvin’s theory on boat wakes would not be applicable. His idea worked in theory, and all the mathematics was proved correct. His research was published in the prestigious Journal of Fluid Mechanics, but there was no empirical evidence at the time of publication. 5 years later, the Ph.D. candidate and a master’s student that he was supervising were able to conduct experiments in a specially engineered tank, and the results backed up the theory.
In fact, these results may have practical applications, such as reducing fuel consumption in ships. Much of the fuel is actually put into generating waves of the boat wake. If there were to exist a solution to minimize the wave production, it would revolutionize the fuel industry for ships.

Conclusion

While the mathematics of water waves is difficult in comparison to sound and light waves, due to the fact that they propagate with a velocity directly proportional to the wavelength, a beautiful phenomenon occurs as a result – the Kelvin wake. Professor Crawford showed that the Kelvin angle can be found through the use of elementary mathematics. Raubad and Moisy showed that at higher velocities, boats may create narrower wakes, but this was still highly debated. Professor Simen Ellingsen later showed that the reason some wakes may have smaller angles is due to shear flow. It is beautiful that the wakes of a duck and a boat may be the exact same shape, regardless of the size or velocity, and how physics and mathematics can help explain these amazing occurrences. The phenomenon exemplifies the elegance of the natural world, as well as having many practical applications, such as reducing fuel consumption and consequently, emissions.

References and Sources

(2019). Retrieved 11 September 2021, from http://www-f1.ijs.si/~rudi/sola/Kelvin_wave%201.pdf

(2019). Retrieved 11 September 2021, from https://www.irphe.fr/~duchemin/Journal_Club/Rabaud20132.pdf

Kelvin wakes. (2021). Retrieved 11 September 2021, from https://www.itp.uni-hannover.de/fileadmin/itp/emeritus/zawischa/static_html/KWake.html

New Experiments Prove the Physics of Ship’s Wakes. (2021). Retrieved 11 September 2021, from https://www.maritime-executive.com/editorials/new-experiments-prove-the-physics-of-ship-s-wakes

Noblesse, F., Zhang, C., He, J., Zhu, Y., Yang, C., & Li, W. (2016). Observations and computations of narrow Kelvin ship wakes. Journal Of Ocean Engineering And Science, 1(1), 52-65. doi: 10.1016/j.joes.2015.12.005

Physicists rethink the celebrated Kelvin wake pattern for ships. (2013) Retrieved 11 September 2021, from https://physicsworld.com/a/physicists-rethink-celebrated-kelvin-wake-pattern-for-ships/