Written by Karthik Prasad

Introduction 

Perimeter and area are two fundamental values associated with any 2D figure, but how are they related? It seems simple, but it turns out that this question is much more complicated than most have previously thought—it took mathematicians thousands of years to resolve. But, it’s not just complicated: the relation between area and perimeter appears in fields such as classical mechanics, quantum physics, and advanced geometry, and as such is very important. Letting A be the area and P the perimeter, the isoperimetric inequality states that 4AP21 for every closed 2-dimensional figure, and that this relationship generalizes to various other very interesting mathematical structures, like the n-th dimensional real numbers. So, what are we waiting for? Let’s explore some mathematics!

History

In two-dimensions, the isoperimetric inequality essentially asks “given all the closed curves with some perimeter, which one has the maximal area?”. Now, this question has been asked since the beginning of mathematics itself. The legend of the Phoenician princess Dido tells the story of a princess who was given a length of rope to enclose an area as her territory. The question is then, what shape maximizes this area? The answer was theorized to be a circle, but for around two thousand years, the answer remained unknown.

The same idea from the isoperimetric inequality shows up in physics—what is the maximal area for a perimeter is equivalent to the question of what is the minimum perimeter given a certain area. This idea of minimizing a parameter—called the principle of least action, the least amount of work necessary to achieve some change—is hugely important in physics. It is the foundation of Lagrangian and Hamiltonian mechanics, which are the formulations of physics that allow us to solve advanced classical systems and even approach basic quantum mechanical systems. 

Figure 1

Depiction of Princess Dido Laying Rope Around Carthage

Source: [Worldhistory.org – https://www.worldhistory.org/uploads/images/14289.png] 

The Solution

The problem was finally approached for the first time in 1838 by Jacob Steiner, a Swiss geometer. It relied on two principles – the idea that a non-convex shape can be made convex by “flipping” the dents, and that any elongated convex shape can be made more round, increasing area while keeping the perimeter the same. But then, any figure in the plane can be made convex, and then any elongated convex shape can be made more round with the same perimeter, and this increases the area. So, the maximal area should be given when we round the shape as much as possible—and the most round shape is the circle. Therefore, the figure with the most area per perimeter should be a circle. The mathematical formulation of these ideas is called Steiner symmetrization, and can be generalized to the n-th dimension. 

However, Steiner symmetrization didn’t fully prove the inequality by itself—they still had to rigorize the ideas of Steiner Symmetrization and apply it to the isoperimetric problem. Eventually, other mathematicians did this, completing the proof of the isoperimetric problem. Letting A being the area and P the perimeter, mathematicians’ long-held conjecture was finally proven true:  4AP21. The ideas from Steiner symmetrization are depicted in the below image:

Figure 2

Depiction of “Flipping a Dent” and “Rounding the Curve” 

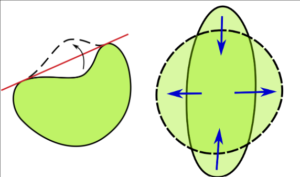
Source: [Oleg Alexandrov – https://commons.wikimedia.org/wiki/File:Isoperimetric_inequality_illustr2.png, https://commons.wikimedia.org/wiki/File:Isoperimetric_inequality_illustr1.svg]

Extension

It turns out that different isoperimetric inequalities hold in higher dimensions. This isoperimetric equation in higher dimension is the following: given dimension n, surface area A, volume S, and volume of a sphere in the n-th dimension B, we have nS(n-1)/n B1/n A, and that both sides of the equations are equal when the figure is a sphere. What is higher-dimensional volume and area? There is no good answer to that question, but a common view is that higher-dimensional volume represents “how much is there”, while area represents “how much is enclosing it”.  Additionally, the isoperimetric inequality has been solved for things that aren’t our regular real numbers as well. On Hadamard manifolds (spaces that look locally like the real numbers), the previous isoperimetric inequality has been proved in dimensions 3 and 4 as well, and many conjectures exist for other spaces.

Conclusion 

In this article, we have discussed the history, solution, and extensions of the isoperimetric inequality. The legend of princess Dido and the city of Carthage, the backstory of Steiner symmetrization, and the extension of isoperimetric inequalities to Rn and Hadamard manifolds revolutionized modern geometry. The isoperimetric inequality shows up in various places in mathematics, and is an incredibly interesting result considering what it means for many other problems.

References and Sources

Source 1  Beltrán, C., & Olmo, I. (2021, January 4). Sobre Mates y Mitos. El País. https://elpais.com/ciencia/2021-01-04/sobre-mates-y-mitos.html 

Source 2  Feynman, R. (n.d.). The Principle of Least Action. The Feynman Lectures on Physics Vol. II Ch. 19: The Principle of Least Action. https://www.feynmanlectures.caltech.edu/II_19.html 

Source 3 http://shell.cas.usf.edu/~dkhavins/papers/isoperimetric.pdf