The Big Bang of Primes
Written by: Arun Muthukkumar
Just a few days ago, we found the new largest known prime number: 2^136279841 – 1. The search for large prime numbers has fascinated mathematicians for centuries due to their importance in number theory, cryptography, and computer science. Prime numbers, defined as numbers divisible by only 1 and themselves, become increasingly rare as numbers grow larger. As a result, mathematicians started using sophisticated algorithms and computational methods to find new primes. One focus of this search is identifying Mersenne primes, a special class of primes of the form 2p – 1 which are some of the largest known primes. The quest for these massive primes not only pushes mathematical boundaries but also drives advancements in our computing capabilities.
Old Primes vs New Primes
The pursuit of large prime numbers dates back to ancient Greece, with mathematicians like Euclid proving that there are infinitely many primes. However, finding larger primes remained a mystery for centuries. This pursuit was fueled by the challenge of identifying patterns within primes, which seemed to appear randomly without a clear formula. Over time, this fascination evolved as primes became central to number theory and its various applications. In the 17th century, Marin Mersenne studied primes of the form 2p – 1 (like 3, 7, and 31), laying the foundation for the modern search for Mersenne primes.
With the advent of computers, the search for primes intensified. In the mid-20th century, algorithms like the Lucas-Lehmer primality test were discovered, allowing researchers to verify enormous primes efficiently. The desire to find large primes is not purely theoretical—primes are integral to modern encryption systems such as RSA, which secure online communications. As prime numbers grow, they offer greater security, fueling the ongoing search. Furthermore, the discovery of each new prime has symbolic value, representing a milestone in human ingenuity and the power of computational mathematics.
2^136279841 – 1
The Great Internet Mersenne Prime Search (GIMPS) has made a significant breakthrough with the discovery of the largest known prime number, 2^136279841 – 1, which boasts an astonishing 41, 024, 320 digits. Found by Luke Durant on October 12, 2024, this new prime surpasses the previous record by over 16 million digits and is only the 52nd Mersenne prime ever discovered. GIMPS, initiated in 1996, leverages the collective power of thousands of volunteers using free software to search for these mathematical rarities.
Recent advancements in technology have revolutionized the search; the rise of Graphics Processing Units (GPUs) has dramatically increased computational capabilities. Durant, utilizing a “cloud supercomputer” composed of thousands of GPUs across 17 countries played a key role in this achievement. The verification of the new prime involved multiple rigorous tests, underscoring the collaborative effort of the GIMPS community. This remarkable find not only demonstrates the capabilities of modern computing but also continues the centuries-long fascination with prime numbers, revealing the ongoing quest to uncover the mysteries of the mathematical world.
Figure 1
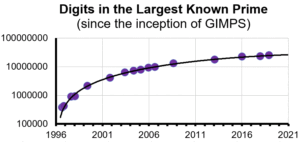
Source: PrimePages
The Future
The search for larger prime numbers has not ended and won’t end anytime soon. What we have in store is quantum computing, a small field with huge potential. Recent advances have uncovered potential connections between prime number theory and quantum physics, offering a promising avenue for further investigation.
Traditional methods for finding prime numbers, like the Sieve of Eratosthenes and the AKS test, can be slow, especially for large numbers. However, a recent study by Southier and colleagues offers a faster solution by using quantum mechanics. They looked at how two quantum systems interact, or become “entangled,” and found that measuring these systems can help identify prime numbers. By examining how the quantum states behave, they created a new algorithm that can find prime numbers much more quickly, in what’s called “polynomial time.” This is a significant improvement over older methods. This discovery highlights the potential of quantum computing to solve mathematical problems more efficiently, opening the door for future research and advancements in the field.
Figure 2
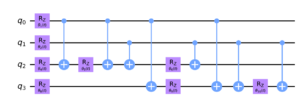
Source: Arxiv
Note: This is a quantum circuit, like the one used by Southier and colleagues.
Conclusion
All of this effort advances other fields more than math. Computing has greatly improved because of the various algorithms that people have developed for primes. Even fields like quantum mechanics have had scientific breakthroughs because of prime numbers. Even biology is related to prime numbers! Both DNA and prime numbers are random but may contain certain hidden structures. You may not know it, but primes affect you.
The discovery of the largest known prime number, 2^136279841 – 1 is a landmark in the search for prime numbers. For most researchers, this accomplishment is a testament to how far humanity has come.
References and Sources
Source 1 A. L. M. Southier, L. F. Santos, P. H. S. Ribeiro, and A. D. Ribeiro, Identifying primes from entanglement dynamics, Phys. Rev. A 108, 042404 (2023).
Source 2 “Arxiv” https://arxiv.org/html/2403.14703v1
Source 3 “Mersenne Prime Number discovery – 2136279841-1 is Prime!” https://www.mersenne.org/primes/?press=M136279841.
Source 4 (N.d.). Retrieved from https://www.youtube.com/watch?app=desktop&v=sD0NjbwqlYw
Source 5 “PrimePages” https://t5k.org/notes/by_year.html#:~:text=By%201876%20Lucas%20had%20developed,%2D1%20%3D%20170141183460469231731687303715884105727%20was%20prime.