Imagine a shape so intricate that it reveals infinite complexity as you zoom in on a structure where patterns repeat endlessly at every scale. These mesmerizing forms, known as fractals, defy traditional geometric conventions and open a gateway to understanding natural patterns. From the jagged edges of a coastline to the delicate structure of a snowflake, fractals bridge mathematics and the natural world. But what are fractals, how are they generated, and why do they matter in science, technology, and beyond?

What are they?

In mathematics, a fractal is a mathematical set defined by its self-similarity, meaning its structure doesn’t change under magnification. Exact self-similarity only appears in purely mathematical fractals, such as the Koch snowflake, where the pattern repeats perfectly. However, natural fractals, such as coastlines and mountain ranges, only exhibit statistical self-similarity, where repetition is approximate and follows probabilistic rules.  This infinite detail allows fractals to defy traditional methods of measurement, such as the perimeter. In the Koch snowflake, for example, the perimeter grows infinitely large as the measuring unit becomes smaller. 

Figure 1

A Koch snowflake starting from an equilateral triangle, shown after three iterations: each side divided and adorned with smaller outward-pointing triangles, forming a detailed, jagged snowflake-like fractal. 

Source: Wolfram MathWorld 

Unlike traditional Euclidean shapes with integer dimensions, fractals often have non-integer dimensions, called their fractal dimension. The fractal dimension quantifies the complexity of a fractal by describing how it scales across different magnifications. For instance, the Koch curve is created by replacing the middle third of a line segment with two additional segments that form an equilateral triangle. Repeating this process indefinitely generates a jagged curve with infinite detail. To calculate the Koch curve’s fractal dimension, it can be divided into 4 self-similar segments with each being scaled down by a factor of one-third. Expressing the relationship of these factors mathematically gives us the equation (⅓)-D = 4, with D representing the fractal dimension. Solving this equation finds that the fractal dimension of the Koch curve is about 1.2619, representing the added complexity beyond a one-dimensional line. 

Generating fractals typically involves the use of iterative processes, repeatedly applying simple mathematical rules to create complex patterns. Some fractals, such as the Sierpinski triangle or Cantor set, are created through geometric replacement rules, while others, like the Mandelbrot set, are created from escape-time algorithms that apply iterative equations to determine if a point in the complex plane belongs to the fractal set. The Mandelbrot set, for example, is defined by the equation zn+1 = z2n + c where z is a complex number and c is some constant, creating the graph shown in figure 2. Random fractals, produced through stochastic processes (models that describe the evolution of random quantities over time or space) like Brownian motion, can often be used to model natural phenomena such as terrain formation or particle diffusion.

Figure 2

An image of the Mandelbrot set

Source: FractalFoundation

History

The mathematics behind fractals began to take shape when Gottfried Leibniz started to think about recursive self-symmetry in the 17th century. However, it would take two centuries to find the first function whose graph would be considered a fractal by modern standards. Having the counter-intuitive property of being continuous everywhere and differentiable nowhere, Karl Weierstrass presented the first fractal at the Royal Prussian Academy of Sciences in 1872. In 1883, Georg Cantor introduced the Cantor set, a set of points lying on a single line segment, notable for being uncountably infinite yet having zero length, which was later recognized as a fractal. Around the same time, Felix Klein and Henri Poincaré introduced a new category of fractals called self-inverse fractals (a fractal that acts as its own inverse scaled up or down). In 1904, Helge von Koch defined the Koch snowflake, followed by Wacław Sierpiński’s famous triangle and carpet in 1915-1916. By 1918, Pierre Fatou and Gaston Julia independently discovered fractal behavior in complex number mappings, leading to the study of attractors (points or sets toward which iterations converge) and repellers (points or sets from which iterations diverge), laying the foundation for the study of dynamical systems.

In 1918, Felix Hausdorff expanded the definition of dimension, allowing for non-integer dimensions, essential for the concept of fractals. Paul Lévy further developed the idea of self-similar curves in 1938 with the Lévy C curve. Manual drawings limited early fractal research, but with the advancements of modern computer graphics in the 1960s, researchers like Benoit Mandelbrot made significant advancements in fractal research. In 1975, Mandelbrot coined the term “fractal” and used computer visualizations to show his definition, called the Mandelbrot set, which was also a fractal. By 1980, Loren Capenter’s SIGGRAPH presentation showcased new software able to generate never-seen-before fractal landscapes.

Figure 3

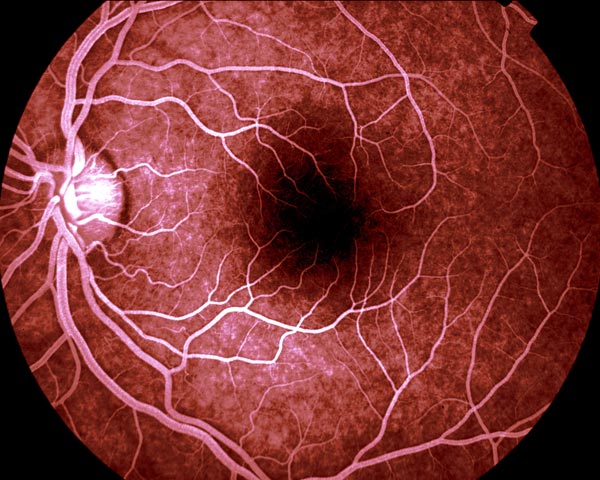
Blood vessel fractals

Source: FractalFoundation

Applications

In nature, fractals appear in various branching structures like trees, blood vessels, and neurons, along with coastlines, mountain ranges, and cloud formations. Understanding fractals helps us model these structures, allowing us to solve complex tasks like estimating the carbon content of trees through branching analysis or understanding geological formations and weather patterns. In technology, fractals improve the design of antennas, heat exchangers, and digital imaging systems. They are especially useful for procedural generation in computer graphics, allowing us to create realistic terrains and textures in video games and films. Additionally, medicine benefits from fractal modeling in diagnostic imaging, neuroscience, and pathology, where fractals represent cellular structures and brain activity.

Conclusion

Fractals offer a unique perspective on the nature of our world, bridging mathematics with nature and technology. Their infinite complexity and self-similar structures provide tools to understand, model, and create intricate systems across diverse fields. Whether used for scientific research, technological innovation, or artistic inspiration, fractals represent the beauty of mathematics and its connection with our universe. As our understanding and computational power continue to grow, fractals will undoubtedly inspire new discoveries and applications, allowing us to view our world in a new way.

References and Sources

Falconer, K. J. (2003). Fractal geometry: mathematical foundations and applications. Wiley.

Fractal Foundation. (2009). What are Fractals? – Fractal Foundation. Fractalfoundation.org; Fractal Foundation. https://fractalfoundation.org/resources/what-are-fractals/

Mandelbrot, B. B. (1983). The Fractal Geometry of Nature. Times Books.

Mathigon. (n.d.). Fractals. Mathigon. https://mathigon.org/course/fractals/introduction

Weisstein, E. W. (n.d.). Koch Snowflake. Mathworld.wolfram.com. https://mathworld.wolfram.com/KochSnowflake.html