Written by: Karthik Prasad

The real numbers are something every math student is familiar with—after all, they are the numbers that make up the real world itself. However, we often take the existence and structure of these numbers for granted. We will discuss the whole numbers, the integers, construct the rational numbers, and then discuss what makes the real numbers special amongst these.

Addition and The Integers

First, let us discuss the whole numbers. These are 0, 1, 2, … and are simple to imagine in the real world—we can consider them as the amount of a certain object we have. You have zero cookies (none at all), one cookie, two cookies, etc. Now, the whole numbers are imbued with a couple of properties. The first is associativity: a+(b+c) = (a+b)+c. The second is commutativity: a+b = b+a. Finally, the zero identity property: a+0=a. These hold for all natural numbers. For example, if you have 2 cookies, and add them to a group of 3 and 4 cookies, this is the same as adding 2 cookies and 7 cookies to get 9 cookies, But, you could also have a group of 2 and 3 cookies first to get 5 cookies, and then add 4 to get 9 cookies as well. Similarly, if you have 2 cookies and 3 cookies, that’s the same as 3 cookies and 2 cookies—and if you have 0 cookies and 2 cookies, then you still have 2 cookies.

However, we may also “owe” other people cookies. In this case, we want to quantify the idea of a negative number—if we owe someone a cookies, then we effectively have some new “negative” amount x of cookies. If we gain a cookies, we imagine giving these a cookies to the other person, and then we have 0 cookies left over. So, we have that a+x = 0 for all a, and that for any a, there is always an x that does this, as you can always give away your cookies. We say x is -a and call it the inverse of a. This leads to the property that for every whole a, there is a number -a such that a+-a = 0. This is the inverse property of addition. These above properties are summarized in Figure 1.

Figure 1

Depicts Associativity, Commutativity, Identity, and Inverse Properties of Addition

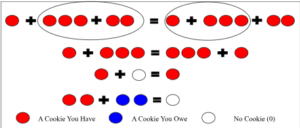
Source: [Original Work]

These lead us to create the integers, which are … -2, -1, 0, 1, 2, … and satisfy these above properties, which are summarized in the table above. Also note that if you have a amount of cookies and b amount of cookies, then a+b is also a valid amount of cookies. This is the closure property of addition. There is also an ordering of the integers, which makes sense—for two amounts of cookies a and b, either a is less than b, a is the same as b, or a is greater than b, and if a cookies is more than b cookies, and if b cookies is more than c cookies, then a cookies is more than c cookies. 

Multiplication and the Rationals

Notably, when we repeat addition multiple times, we create a new operation called multiplication. We say that if we want to add a number b to something a times, then we add a new quantity a⋅b, such that a⋅b = b + b + b+ b (with a b’s). If you think about the same cookie example, this has commutativity, closure, associativity, and also a new property that works with addition. The distributive property says a⋅(b+c) = a⋅b+a⋅c. This makes sense—if we are adding b+c together a times, this should be the same as adding b together a times, adding c together a times, and then adding them together. We also have the identity property with the number 1, as a⋅1 = a (adding a cookies one time gives you a cookies). 

These properties hold on the integers and seem to match up with most of their properties. However, there is one curious omission—an inverse property for multiplication. This property would imply that there must exist a number x such that a⋅x = 1 in accordance with the identity and inverse properties of addition (where 0 is the identity in addition, 1 is the identity in multiplication, and so an inverse property must produce 1 as the inverse of addition produces 0). 

Therefore, we wish to extend the integers to a new set of numbers that includes this inverse. If we have two integers a and b, we define a/b to be a number such that b⋅a/b = a. When we let a = 1, this gives b⋅1/b = 1, giving us an inverse property. This definition holds for all b not equal to 0. To explain why this does not hold for b = 0, consider adding a cookies 0 times for any number a. This gives you 0 cookies total, logically. But, if there was an identity 1/0 for 0, then we would have 0⋅1/0 = 1, but 0⋅1/0 = 0, so this number 1/0 cannot exist. Therefore, we now have the numbers a/b, and note that every integer a is equal to a/1, as 1⋅a/1 = a/1 = a. Therefore, we can make every integer into the form a/b. We call these numbers a/b the rational numbers. 

The properties of associativity, commutativity, and distributivity are summarized in the table below:

Figure 1

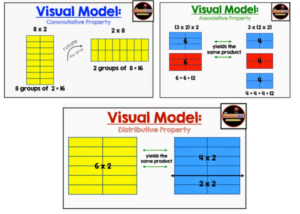
Depictions of Commutativity, Associativity, and Distributivity of Multiplication

Source: [1]

The Real Numbers

These numbers satisfy all the properties of integer addition and multiplication have an inverse property for multiplication, and have the same ordering as the integers do. In the terminology of abstract algebra, this makes rational numbers into a field.  But, there are curious omissions in the rational numbers. For example, the number π, the ratio of a circle’s circumference to its diameter, cannot be written as a/b. Other numbers, such as the number a such that a⋅a = 2, are also not in the rational numbers. To create the real numbers—essentially, the rational numbers PLUS all of the holes in the rationals—we want all of these holes to be filled. 

A mathematical property that achieves this is the least upper bound property, which says that for a set S of real numbers, there exists a least upper bound—an element in S bigger than all the other elements—and that this least upper bound is also a real number. For example, consider the set S of real numbers a such that a⋅a ≤ 2. The maximal a that works is the a such that a⋅a = 2. As we said before, this is not a rational number—but we define it to be a real number, as it must be the least upper bound of S, and therefore is a real number. For any “hole” in the rational numbers, then, you can construct a set S like this and split the rational numbers as “in S” and “outside of S.” Then, the value that is the least upper bound must be a real number, as in the above example. This can be done formally via the method known as Dedekind cuts, filling in all the holes in the rational numbers.

Conclusion

This article started with a discussion of the whole numbers and reasoned through various properties of an “addition” operation on these numbers. We then extended the whole numbers to the integers to satisfy more properties of addition that we desired and then defined the “multiplication” operation of repeated addition (for integers). This allowed us to extend the integers to the rationals to satisfy more properties of multiplication. Finally, we explained a method for filling in the “holes” in the rationals to create the reals via satisfying the least upper bound property. Now, why is this important? These counting numbers and these real numbers are the foundation of, well, the real world. Our current models of the universe and the things we do daily rely on these numbers, and understanding their properties allows us to explore these models further and more completely, hopefully bringing us to new revolutions in mathematics and science.

References and Sources

Source 1: Properties of Operations: Multiplication – Mr Elementary Math. (2014, November 9). https://mrelementarymath.com/properties-of-operations-multiplication/

Source 2: Schwartz, R. (2014). Dedekind Cuts. https://www.math.brown.edu/reschwar/INF/handout3.pdf