Written by: Aarav Shah

Source: https://www.technologynetworks.com/neuroscience/news/deepmind-ai-used-to-develop-new-math-techniques-356418 

Artificial intelligence (AI) is rapidly transforming the world around us. From facial recognition on our smartphones to the algorithms driving autonomous vehicles, AI’s capabilities appear magical. But beneath the seemingly mystical surface lies a powerful and logical engine: mathematics. Math is more than just a collection of equations; it is the language that enables AI models to function.

Mathematics in AI 

According to Oxford, artificial intelligence “refers to the use of technologies to build machines and computers that have the ability to mimic cognitive functions associated with human intelligence, such as being able to see, understand, and respond to spoken or written language, analyze data, make recommendations, and more.” Essentially, artificial intelligence is about finding hidden correlations in large sets of data and relaying these patterns in a format that humans can understand. The majority of this functionality comes from key mathematical fields. Linear algebra and calculus provide the tools for representing data, optimizing algorithms, and making decisions under uncertainty (Jamal 2024). Probability and statistics play a crucial role in analyzing data, understanding AI’s limitations, and ensuring robust performance. These concepts help build the foundation of all the technology we see being applied in various sectors and have a massive yet unseen impact on the world.

Change with Calculus

Calculus is the mathematical framework for understanding how things change. It plays a key role in optimizing datasets and training machine learning models, as it can calculate gradient descent, which is a fundamental optimization algorithm widely used in training various AI models, especially those involving machine learning. By iteratively adjusting the internal parameters of a model to minimize a cost function, it allows the model to make accurate predictions. It is a versatile tool and can be used with complex models in numerous applications, such as deep learning, neural networks, linear regression, and more (Stahl 2023). Calculus is essential to this algorithm, as concepts such as derivatives allow the cost function to find the optimal solution. Without calculus, AI would be unable to “learn” and improve on its outputs.

Data with Linear Algebra

Linear algebra plays a different role in AI training: representing and manipulating complex data structures, especially in neural networks. AI models often deal with vast amounts of data, from images to sensor readings. Linear algebra provides a way to represent this data in scalars, vectors, matrices, and tensors (Figure 1). A scalar is a quantity that only has magnitude and no direction, and can be used to represent data that is not inherently structured as a vector or matrix, such as size. Vectors can represent individual data points such as pixel values in an image or words in natural language processing. Meanwhile, matrices can be used to represent the intensity of a pixel in image processing and data structures in neural networks. Tensors are able to take the concepts of vectors and matrices to represent multidimensional data, including images that go beyond typical RGB. All of these linear algebra concepts serve as important tools to simplify AI training, allowing these models to sort through massive quantities of data.

Figure 1

A visual representation of different methods of storing data

Source: https://dev.to/mmithrakumar/scalars-vectors-matrices-and-tensors-with-tensorflow-2-0-1f66 

Solving Uncertainty with Statistics

While both calculus and linear algebra are incredibly important, the field of statistics arguably contains the most important tools to train AI models. Machine learning is inherently about using data to make predictions, and statistics provides the methodologies for analyzing any given dataset. For example, hypothesis testing, a statistical method for evaluating claims based on data samples, can help assess the usefulness of AI algorithms (Dsouza 2021). Classification, another statistical concept, can allow AI to make decisions based on classifying data to a category. However, the most important application of statistics lies in models “understanding” the uncertainty of the real world and random chance. Probability theory especially plays an important role in providing AI with the tools to deal with missing values, noise, and randomness in training data, even allowing it to make decisions when faced with incomplete information. Statistical insights are the foundation of AI data-driven decision-making.

Figure 2

A quick breakdown of the different math fields needed for AI

Source: https://www.linkedin.com/pulse/learning-math-machine-mahammad-valiyev 

Mathematical Limitations

Current mathematical approaches are incredibly powerful, but they aren’t without their limitations. One key challenge lies in interpreting the inner workings of complex models, particularly those utilizing deep learning. These models often function as intricate “black boxes,” excelling at tasks but leaving us with little understanding of how they arrive at their conclusions (Figure 1). This lack of transparency can raise concerns about reliability and bias, as it can be difficult to pinpoint where errors or unfair prejudices might be creeping into the AI’s decision-making process. Researchers are actively exploring methods to make these models more interpretable, and advancements in this area will be crucial for ensuring the responsible and trustworthy development of AI.

Figure 3

A diagram depicting the different layers of a neural network, including the “hidden layer”

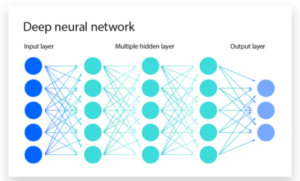
Source: https://www.ibm.com/topics/neural-networks 

The Impact of AI

Although the mathematical concepts that power AI are fascinating, a question arises: what are the impacts of this math on our daily lives? Consider natural language processing (NLP) algorithms like ChatGPT. These AI marvels use vector representations, probabilistic models, and other mathematical tools to generate human-like text. Similarly, computer vision models harness these techniques to “see” the world like us, allowing for object identification. These same technologies and concepts will allow for fully autonomous vehicles, better healthcare diagnoses and treatments, smart appliances, better social media recommendations, and much much more. Thus, fundamental knowledge of mathematics will be invaluable for future AI engineers. As AI continues to evolve, the power of mathematics will remain the invisible engine driving this transformation, shaping the world for centuries to come.

References and Sources

Dsouza, J. (2021, November 24). All the math you need to know in Artificial Intelligence. freeCodeCamp.org. https://www.freecodecamp.org/news/all-the-math-you-need-in-artificial-intelligence/ 

 Google. (n.d.). AI vs. Machine Learning: How do they differ?  |  google cloud. Google. https://cloud.google.com/learn/artificial-intelligence-vs-machine-learning

Jamal, M. (2024, January 19). Why math is vital to thrive in your AI career. Built In. https://builtin.com/articles/math-for-ai  

KCP. (2023, November 7). The crucial role of mathematics in AI development. Medium. https://medium.com/@Noodle_LLC/the-crucial-role-of-mathematics-in-ai-development-dd31d4d6e55c

Nelson, H. (2023). Essential math for AI next-level mathematics for developing efficient and successful AI systems. O’REILLY MEDIA. 

Stahl, A. (2023, May 31). The math behind predictions in AI: Unraveling the magic. Medium. https://medium.com/@stahl950/the-math-behind-predictions-in-ai-unraveling-the-magic-44b4fcb8af6