Untangling Mathematics: A Look Into DeepMind’s New AI
Written by: Gloria Wang
As an expanding field with a wide variety of applications, artificial intelligence (AI) has been a hot topic for decades. Machine learning has been applied to board games, language, and healthcare. But for the first time, researchers have applied AI to math: detecting patterns in knots. Just last month, Google’s DeepMind team— the same team that broke headlines with AlphaGo— released the preprint of their paper “The Signature And Cusp Geometry Of Hyperbolic Knots” on arXiv.
What are Knots?
In day-to-day usage, a knot refers to certain ways to tie some kind of string. But unlike tying shoelaces, a mathematical knot is closed: there are no ends to tie or untie. Thus, they look more like pretzels than shoelaces. Open-ended knots are termed “braids.” In order to be considered a knot, the curves cannot untangle into the unknot, also known as a trivial knot. This knot is literally not knotted— a simple loop; a three-dimensional circle.
Figure 1

Different types of knots. The unknot sits in the top left corner.
Source: Wikipedia
The purpose of knot theory is to understand the geometry of strings: can a tangled string be untangled without having to cut it? Is there a simple way to make these determinations? To answer these questions, mathematicians have spent centuries trying to detangle the mathematics of knot theory. But now, DeepMind’s new AI is helping too.
Math Machine
Although machine learning is not able to explain why the patterns work or even exactly how they work, it can push mathematicians into the general direction of understanding how the patterns work, making it easier for mathematicians to work out the details of a rigorous proof.
In order to train the model, researchers calculated the invariant— a property of knots that “always assigns the same value to equivalent knots”—of millions of knots (Wolfram MathWorld). Researchers then discovered that the most helpful technique to finding patterns that link two properties is saliency maps. This technique is often used in computer vision to reflect the degree of importance for each region within an image. Applied to pattern recognition, saliency maps highlight properties that are likely to be linked and generate a formula that was proved by Lackenby and Juhász.
Figure 2
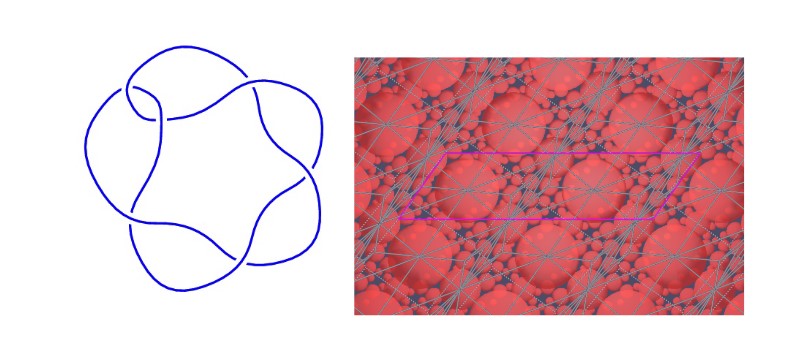
The stevedore knot (left) and its corresponding shape transition (right) provided by SnapPy, a Python-based program used to study the topology and geometry of 3-manifolds, with a focus on hyperbolic structures.
Source: Davies et al., 2021.
With these discoveries, researchers introduced a new, real-valued invariant termed the “natural slope.” This natural slope is defined as the real number subtracted from the longitude a geodesic—the shortest path between two points—travels along the knot and back to the initial meridian. This new invariant introduces new relationships between knot properties, and is applicable to other branches of mathematics such as the Dehn surgery and 4-ball genus.
Figure 3
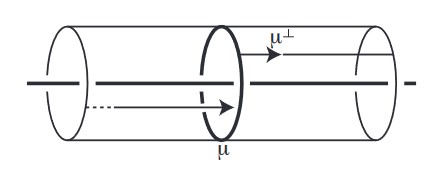
The definition of a natural slope: “A geodesic running in the direction μ⊥ that is perpendicular to the meridian μ. By the time it returns to the meridian, it has travelled one longitude minus some multiple s of the meridian. This real number s is the natural slope of K.”
Source: Davies et al., 2021.
Conclusion
DeepMind’s AI model has proven once again that machine learning has potential far beyond its current applications. Even mathematics, a world rich with intuition and thorough proofs, is now utilizing these technologies to connect the dots and improve efficiency. At the same time, it allows computer scientists to take a glimpse into the abstract reality of mathematics. DeepMind scientist Davies “told reporters that the project has given him a ‘real appreciation’ for the nature of mathematical research. Learning maths at school is akin to playing scales on a piano, he added, whereas ‘real mathematicians’ work is more like jazz improvisations.” Artificial intelligence will continue to push the limits of human intelligence, aiding us in our journey to understand the world around us.
References and Sources
Castelvecchi, D. (2021). “DeepMind’s AI helps untangle the mathematics of knots.” Nature, https://www.nature.com/articles/d41586-021-03593-1
Davies, A., Juhasz, A., Lackenby M., & Tomasev, N. (2021). The Signature And Cusp Geometry Of Hyperbolic Knots. Pre-print at arXiv. https://arxiv.org/abs/2111.15323
Weisstein, Eric W. “Knot Theory.” From MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/KnotTheory.html
Weisstein, Eric W. “Knot Invariant.” From MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/KnotInvariant.html